Big O Notation — BrunoB Notes

Big O notation describes how the runtime or space usage of an algorithm grows with the size of its input. It’s a language-agnostic way to compare solutions and reason about performance at scale.

Why it matters

Predict performance as inputs grow
Choose data structures and algorithms wisely
Focus on scalability, not exact milliseconds

How to read Big O

Drop constants: O(2n) → O(n), O(n + 100) → O(n)
Keep the dominant term: O(n² + n) → O(n²)
Worst vs Average vs Best: Unless specified, Big O often refers to the worst-case.
Amortized: Average cost over many operations (e.g., dynamic array push)

Common growth rates

Class	Big O	Example
Constant	O(1)	Array indexing by position
Logarithmic	O(log n)	Binary search in a sorted array
Linear	O(n)	Traverse all elements
Linearithmic	O(n log n)	Merge sort, quicksort (avg)
Quadratic	O(n²)	Nested loops over same input
Linear Two Variables	*O(NM)**	2D matrix traversal
Exponential	O(2ⁿ)	Naive subset generation
Factorial	O(n!)	Permutations of n items

Quick examples

Array access: Read by index → O(1)
Scan array: Sum all values → O(n)
Binary search: Halve the search space each step → O(log n)
Merge sort: Divide + merge → O(n log n)
Two nested loops: Compare each pair → O(n²)

Amortized O(1): Appending to a dynamic array is O(1) on average, even though occasional resizes take O(n). The average cost over many appends is constant.

Visual examples

Here's how different time complexities look in action:

O(1) - Constant Time

Array access by index - always takes the same time regardless of array size

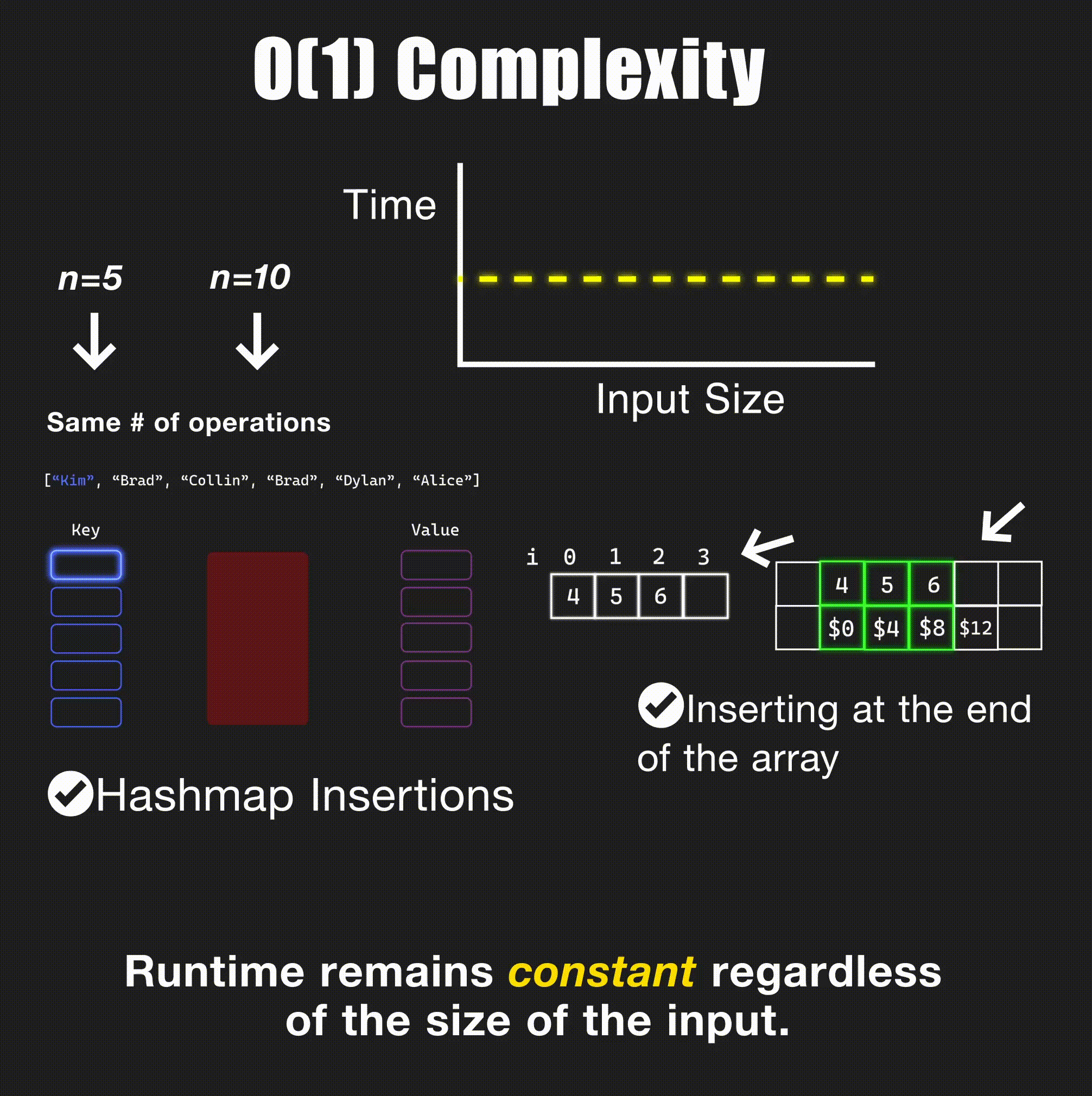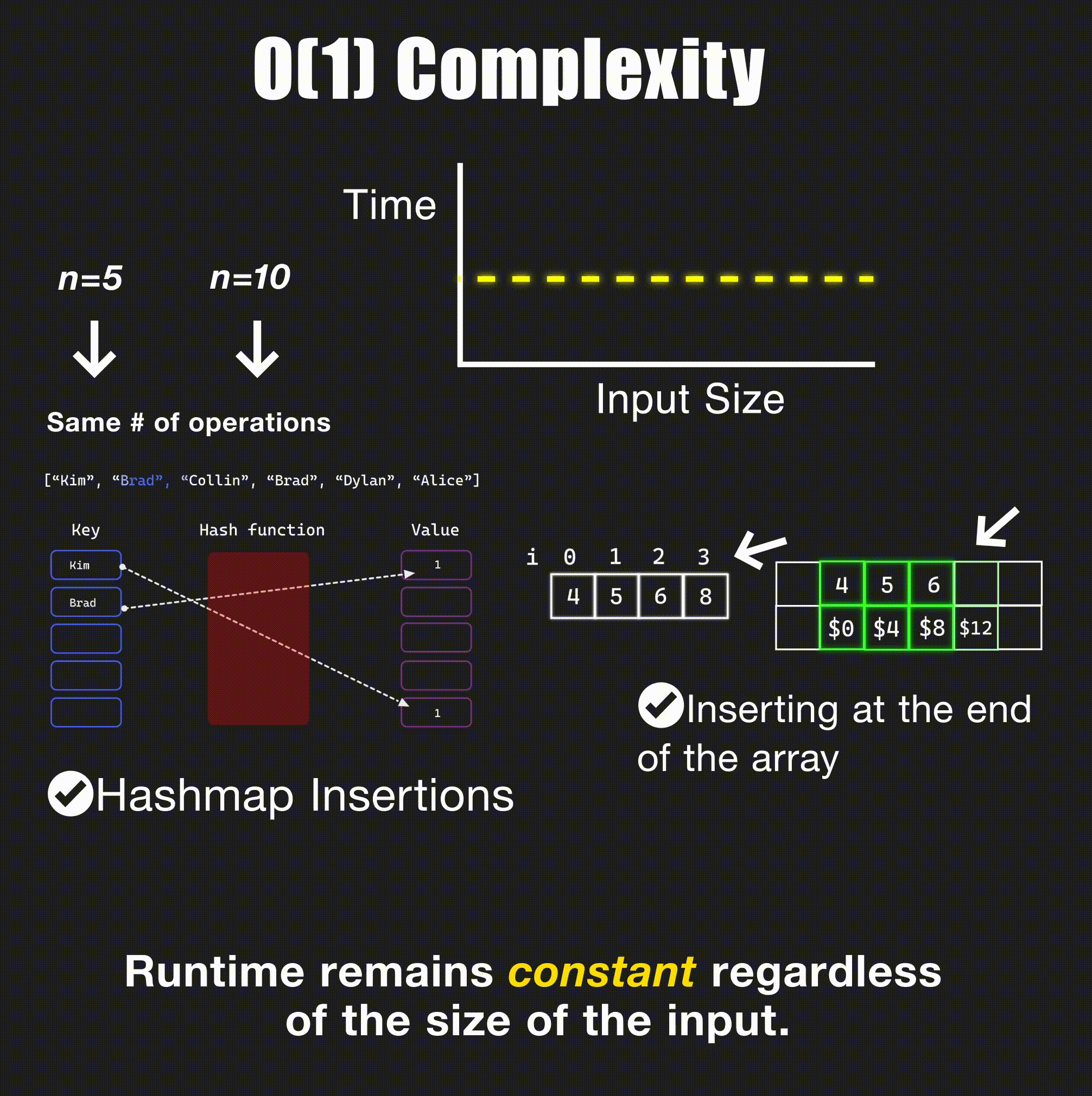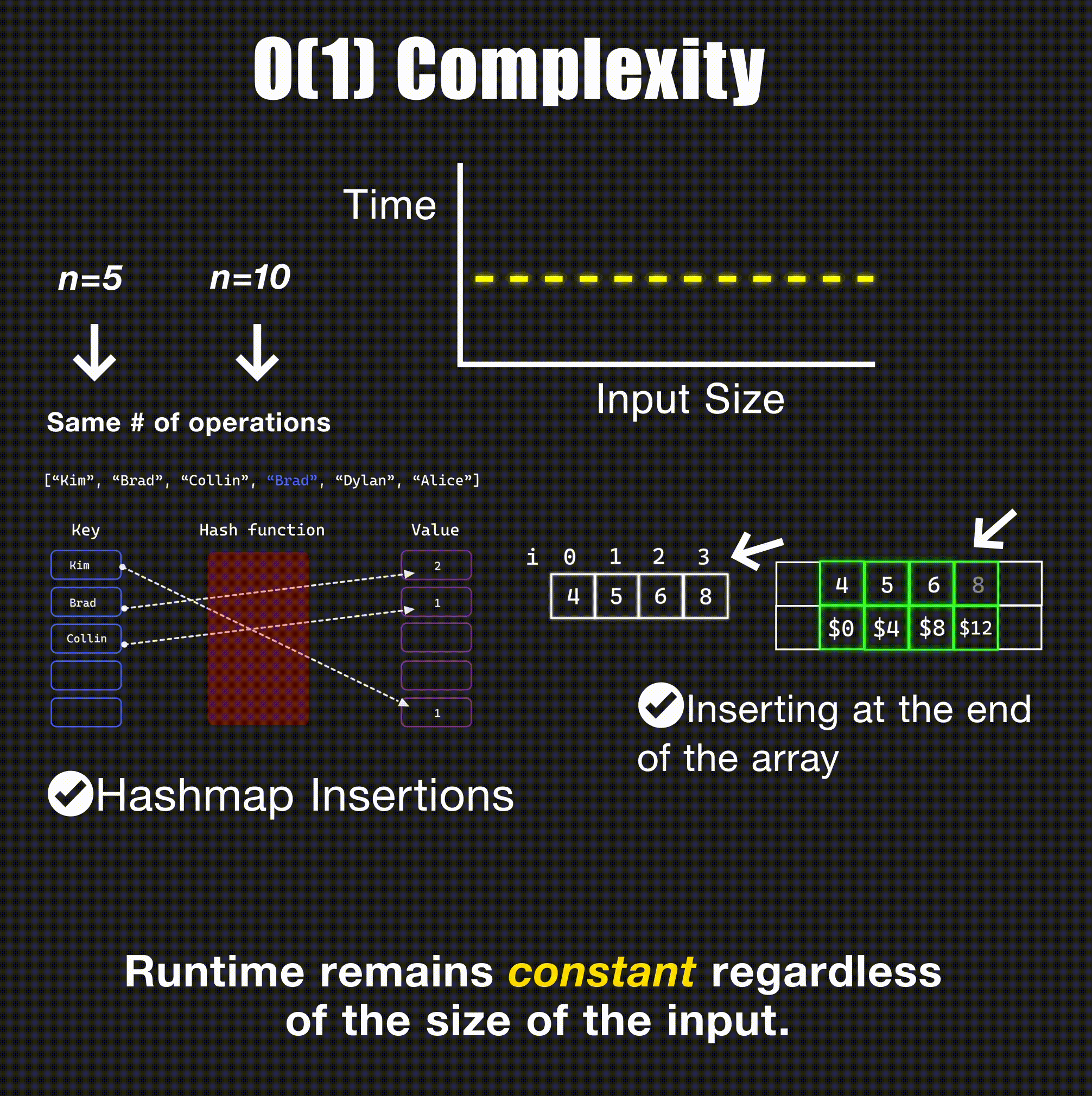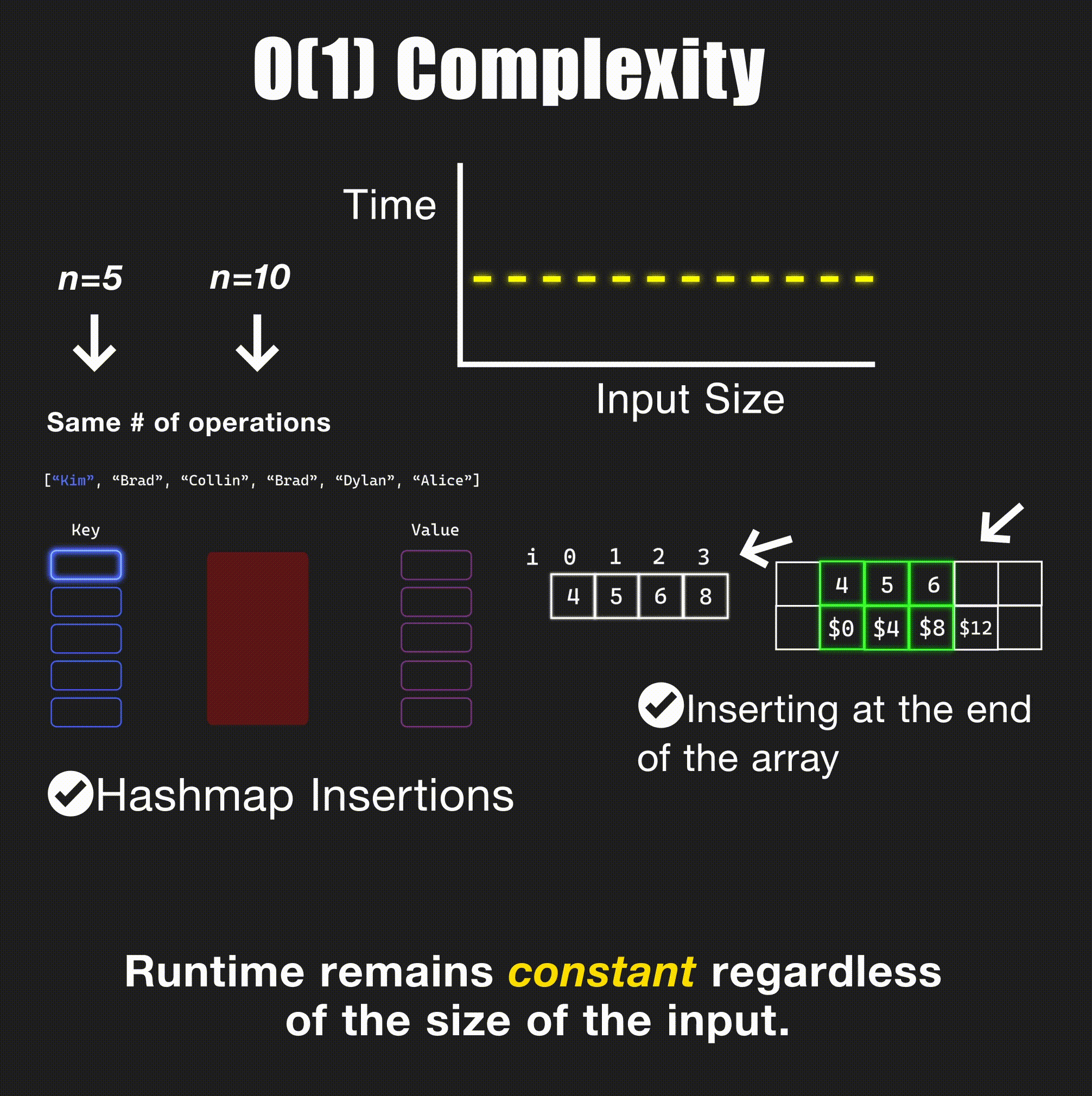
// Accessing array element by index - O(1)
int getElement(int arr[], int index) {
    return arr[index];
}

// Accessing array element by index - O(1)
public int getElement(int[] arr, int index) {
    return arr[index];
}

# Accessing array element by index - O(1)
def get_element(arr, index):
    return arr[index]

O(log n) - Logarithmic Time

Binary search - eliminates half the search space with each step

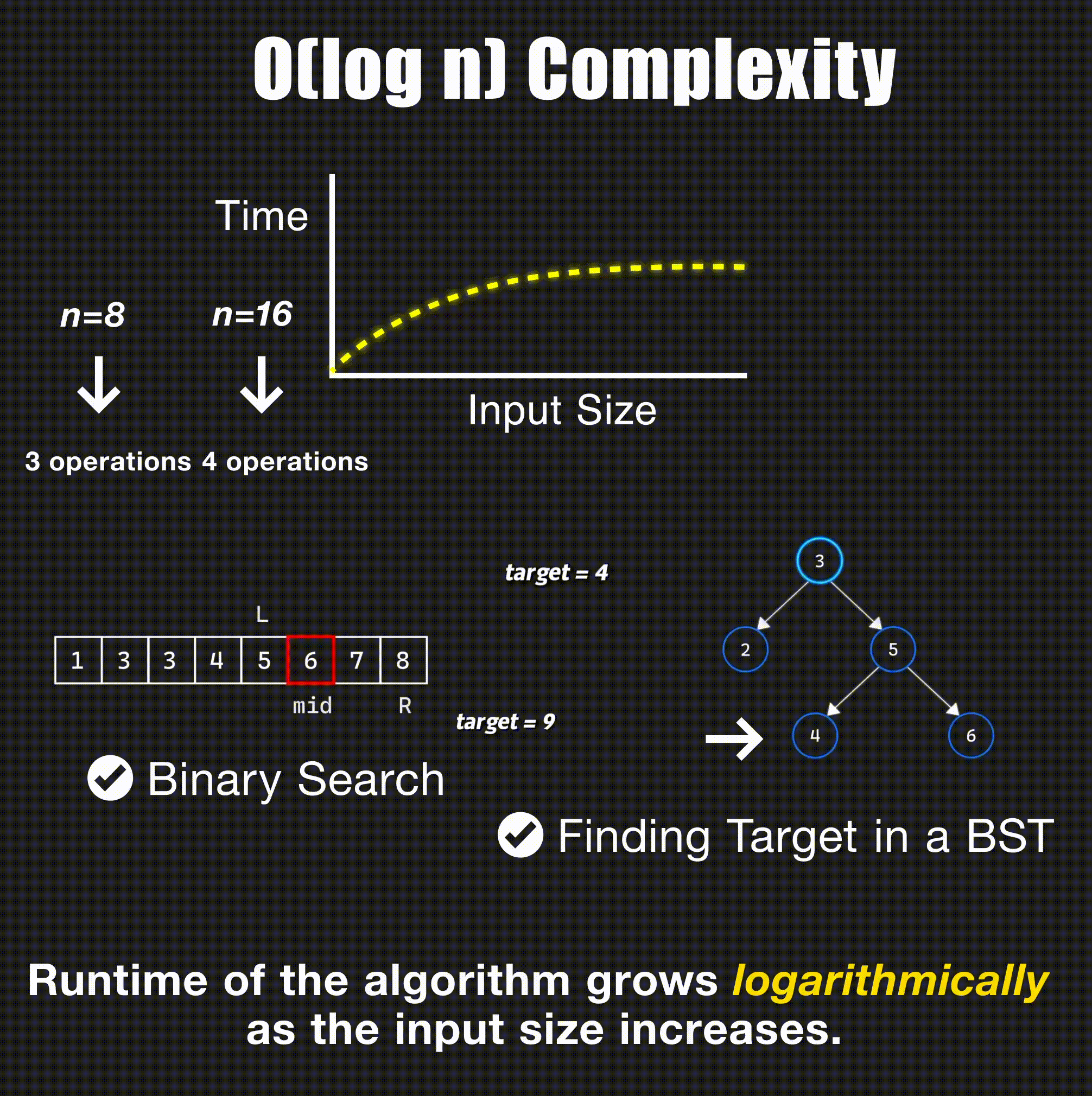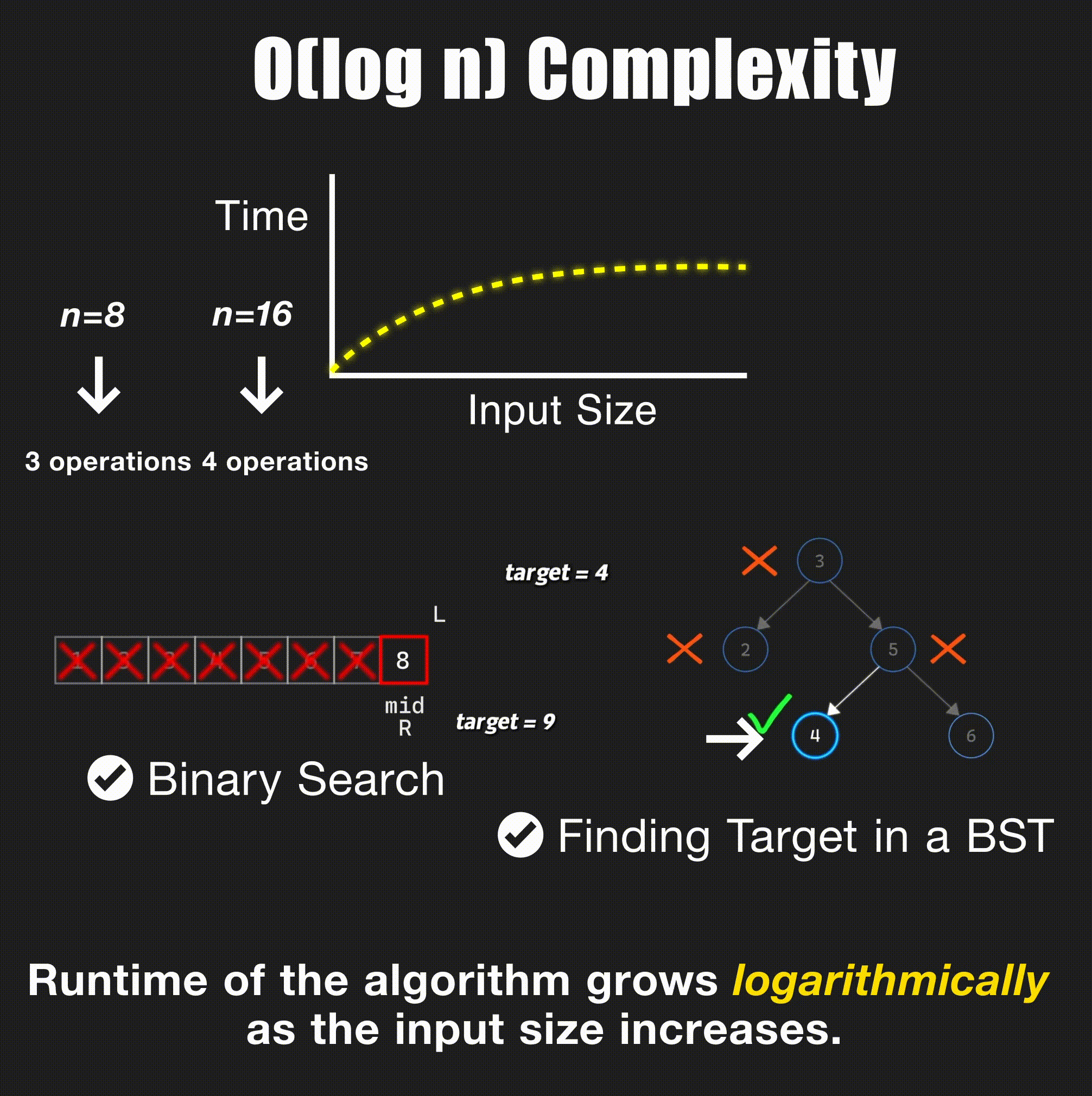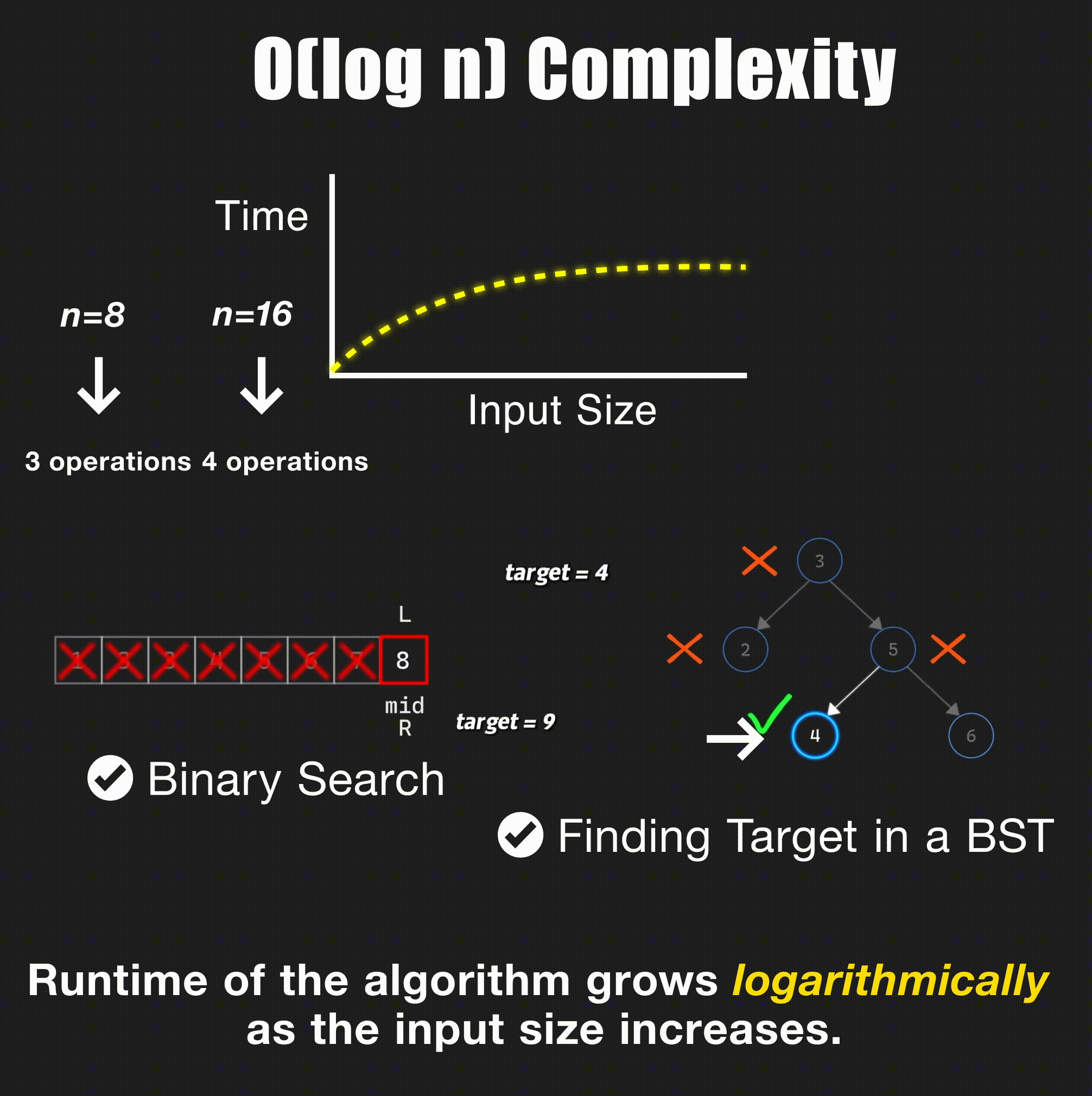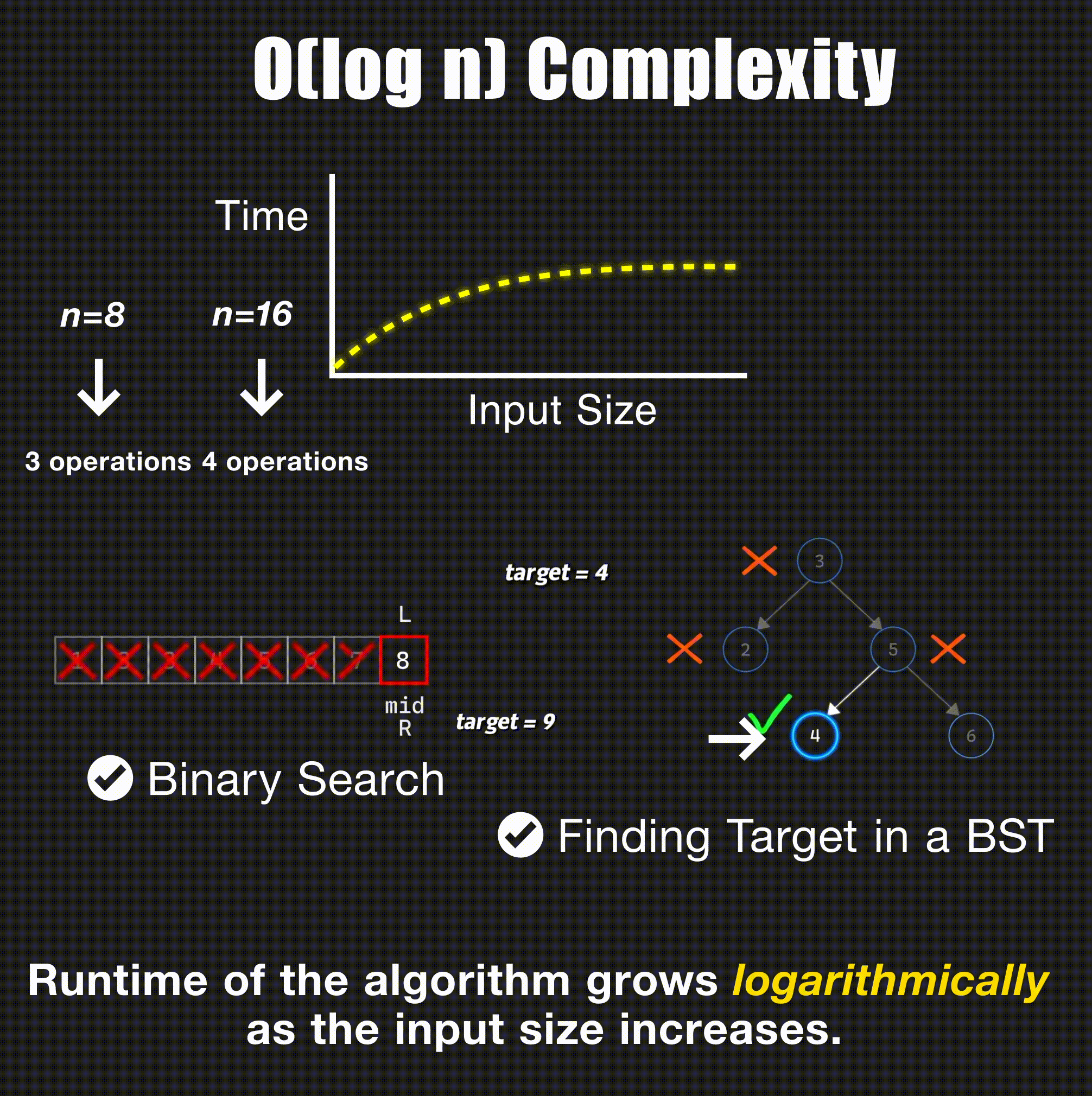
// Binary search in sorted array - O(log n)
int binarySearch(int arr[], int size, int target) {
    int left = 0, right = size - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (arr[mid] == target) return mid;
        if (arr[mid] < target) left = mid + 1;
        else right = mid - 1;
    }
    return -1;
}

// Binary search in sorted array - O(log n)
public int binarySearch(int[] arr, int target) {
    int left = 0, right = arr.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (arr[mid] == target) return mid;
        if (arr[mid] < target) left = mid + 1;
        else right = mid - 1;
    }
    return -1;
}

# Binary search in sorted array - O(log n)
def binary_search(arr, target):
    left, right = 0, len(arr) - 1
    while left <= right:
        mid = left + (right - left) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return -1

O(n) - Linear Time

Array traversal - time grows linearly with input size

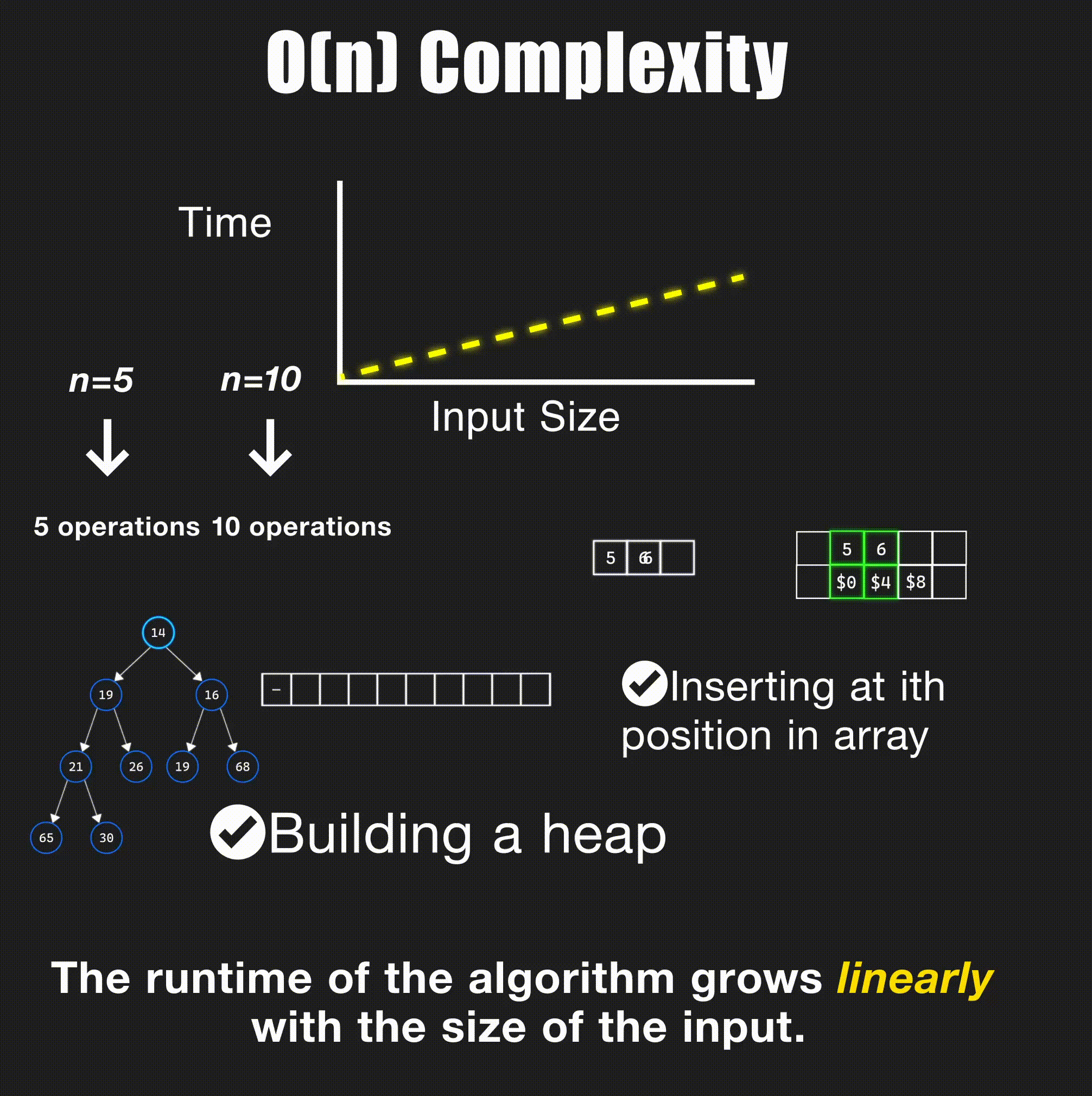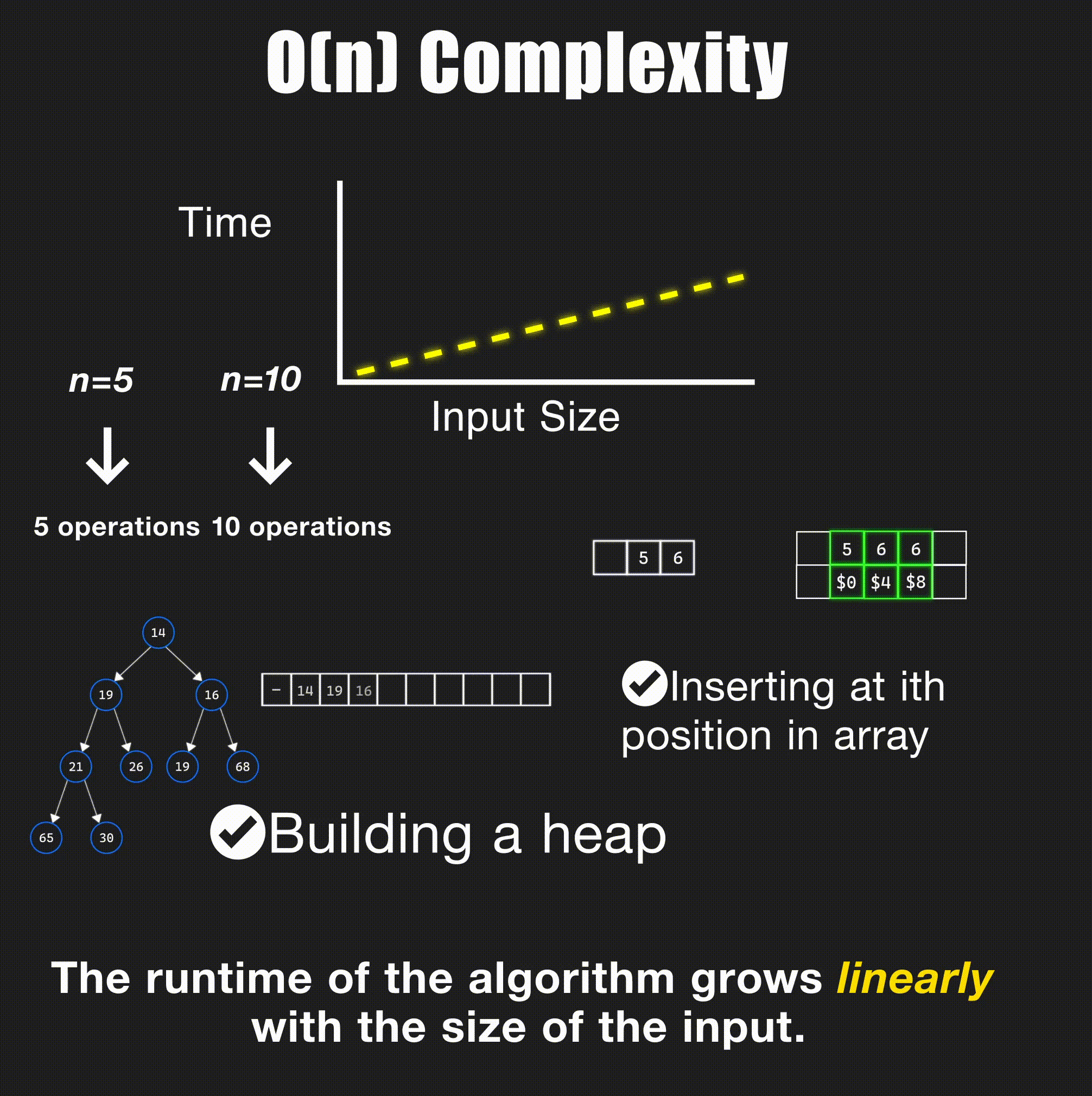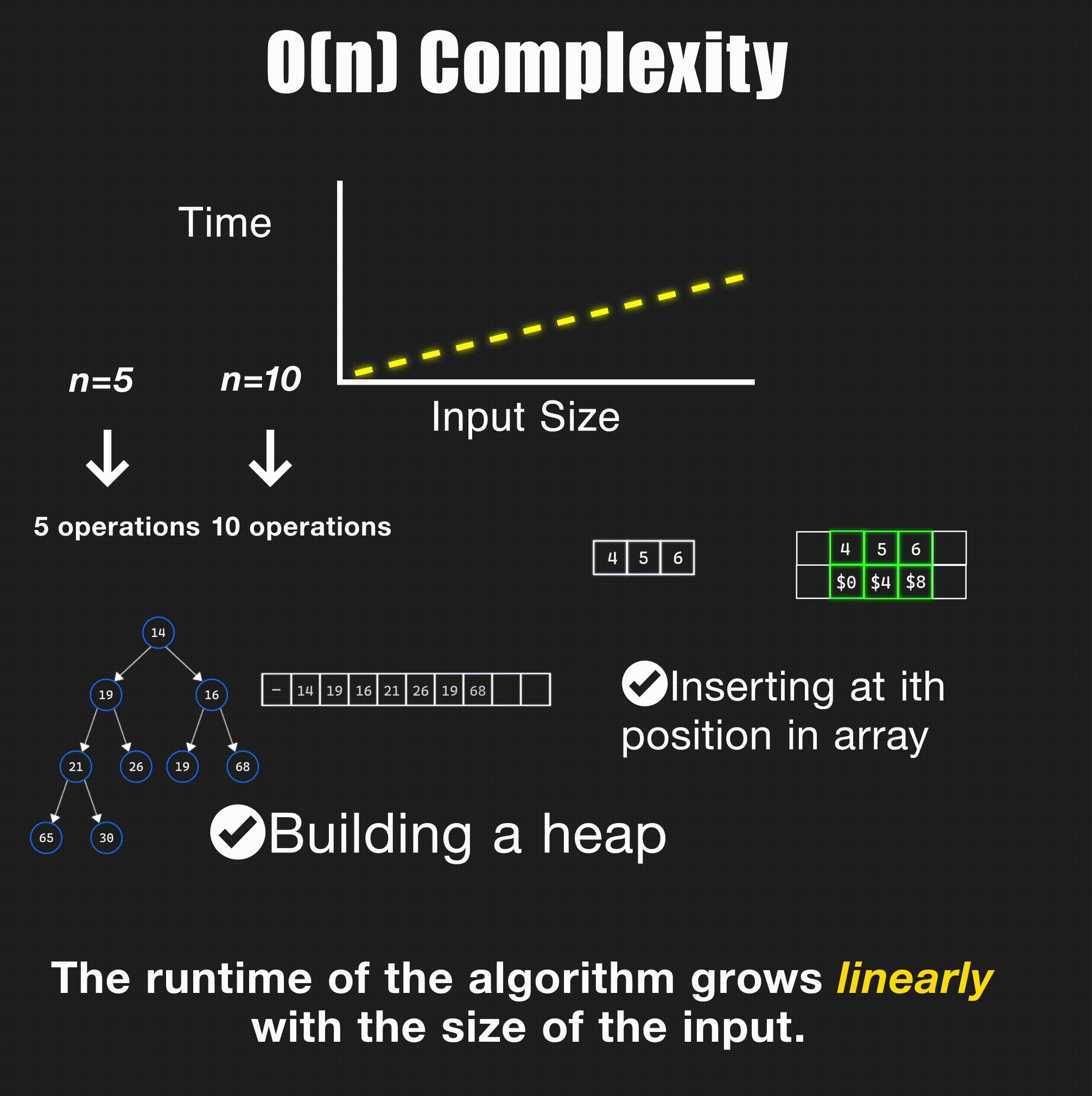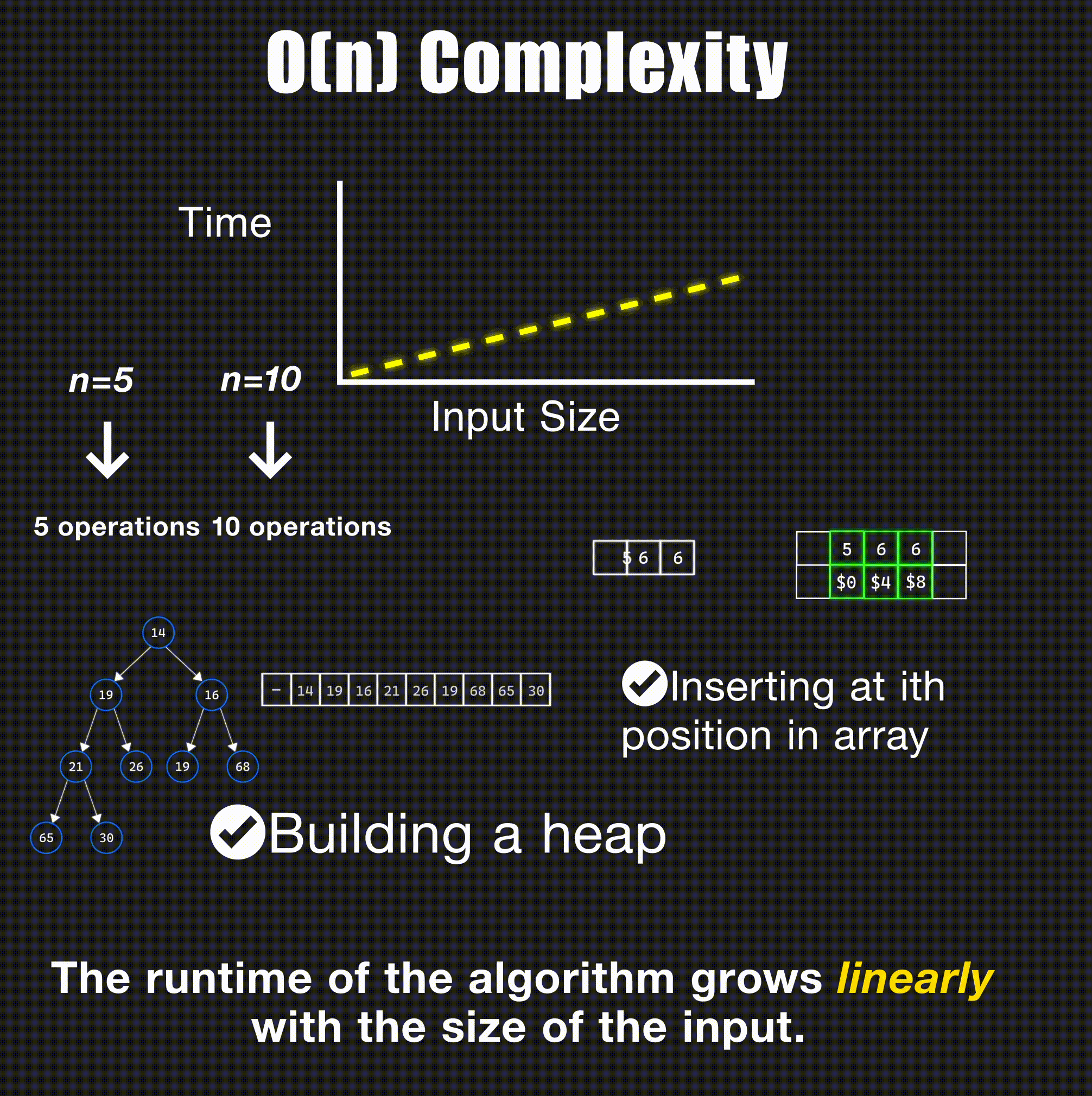
// Linear search through array - O(n)
int linearSearch(int arr[], int size, int target) {
    for (int i = 0; i < size; i++) {
        if (arr[i] == target) {
            return i;
        }
    }
    return -1;
}

// Linear search through array - O(n)
public int linearSearch(int[] arr, int target) {
    for (int i = 0; i < arr.length; i++) {
        if (arr[i] == target) {
            return i;
        }
    }
    return -1;
}

# Linear search through array - O(n)
def linear_search(arr, target):
    for i in range(len(arr)):
        if arr[i] == target:
            return i
    return -1

O(n log n) - Linearithmic Time

Merge sort - divide and conquer approach

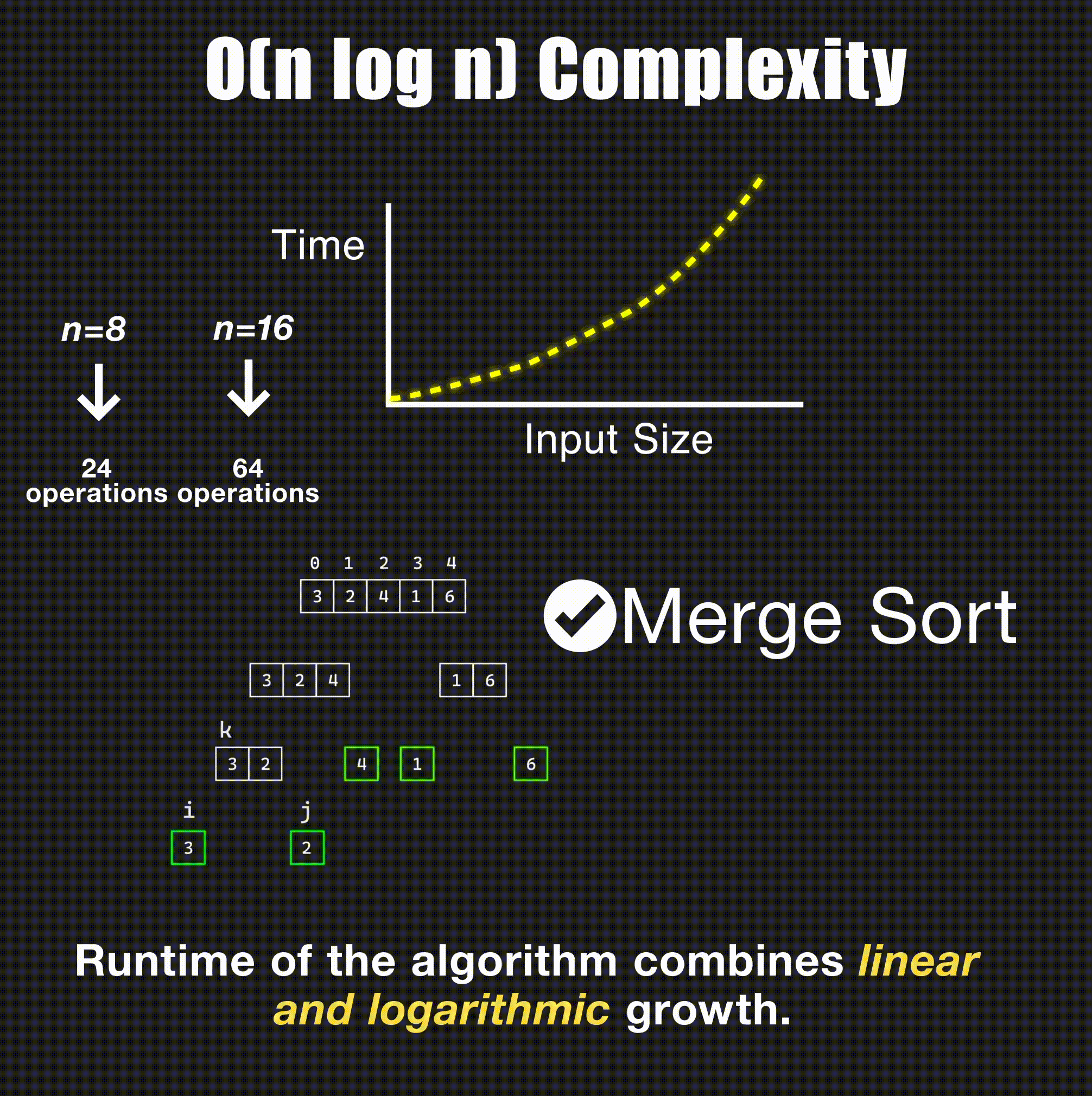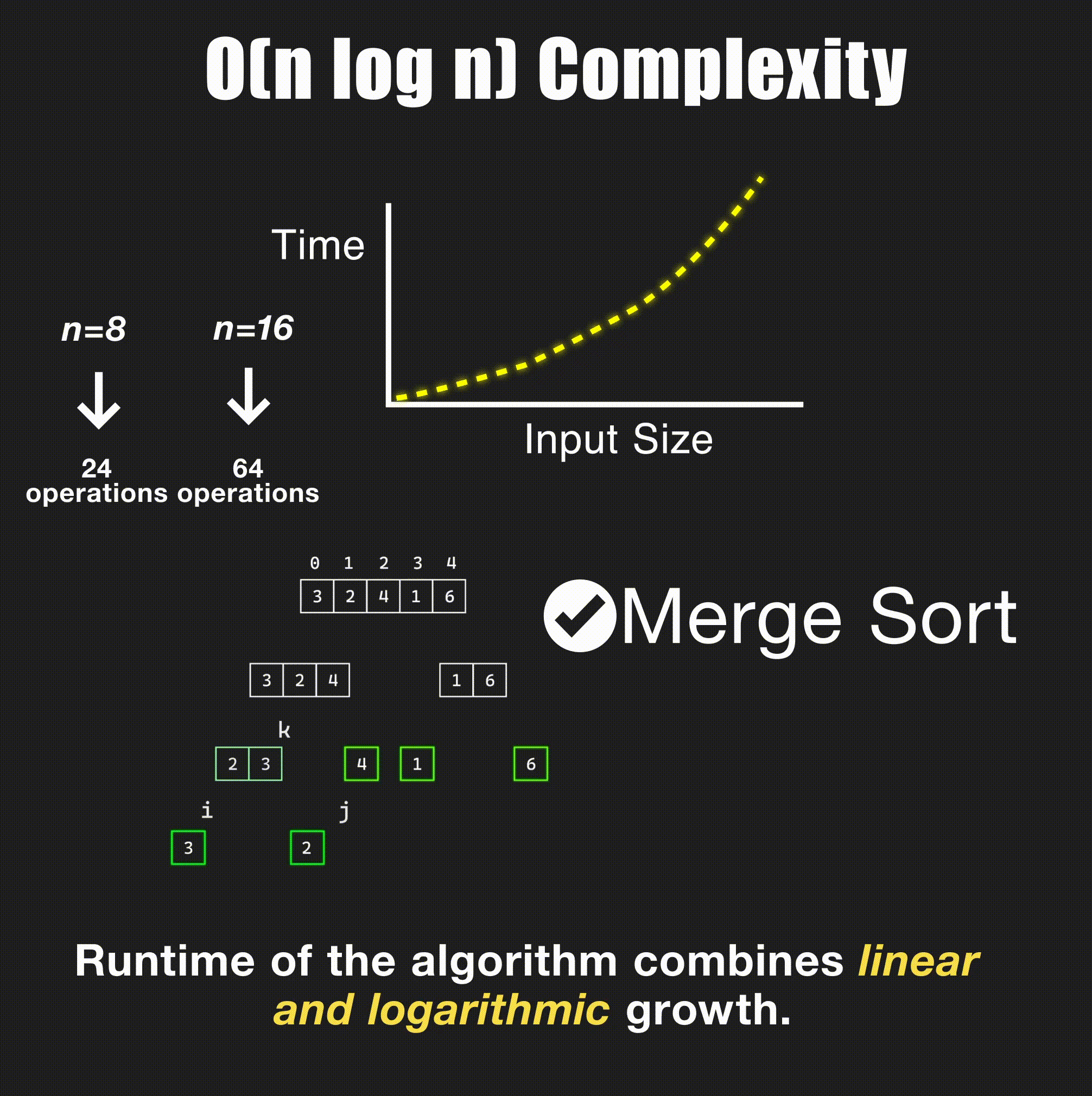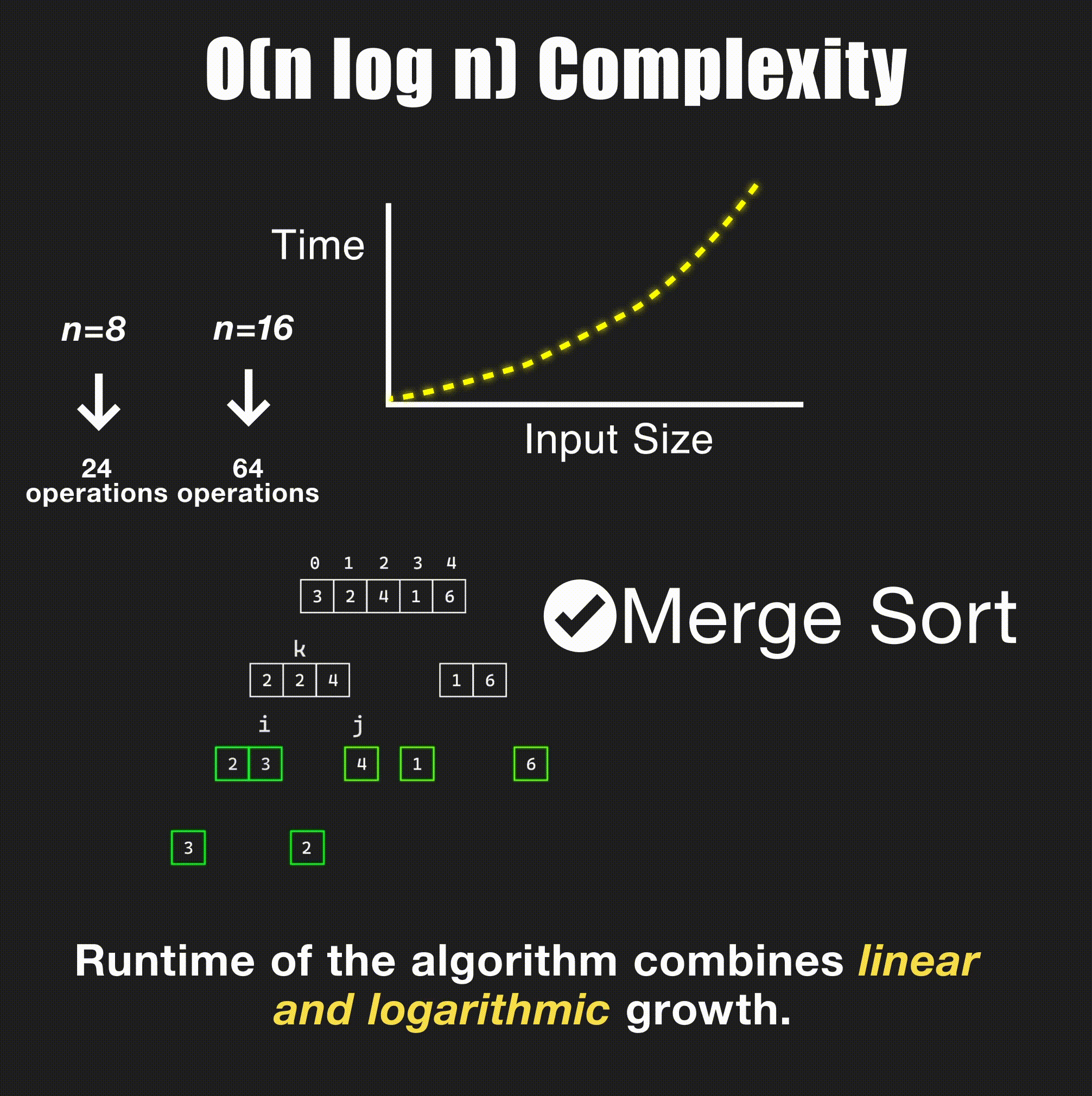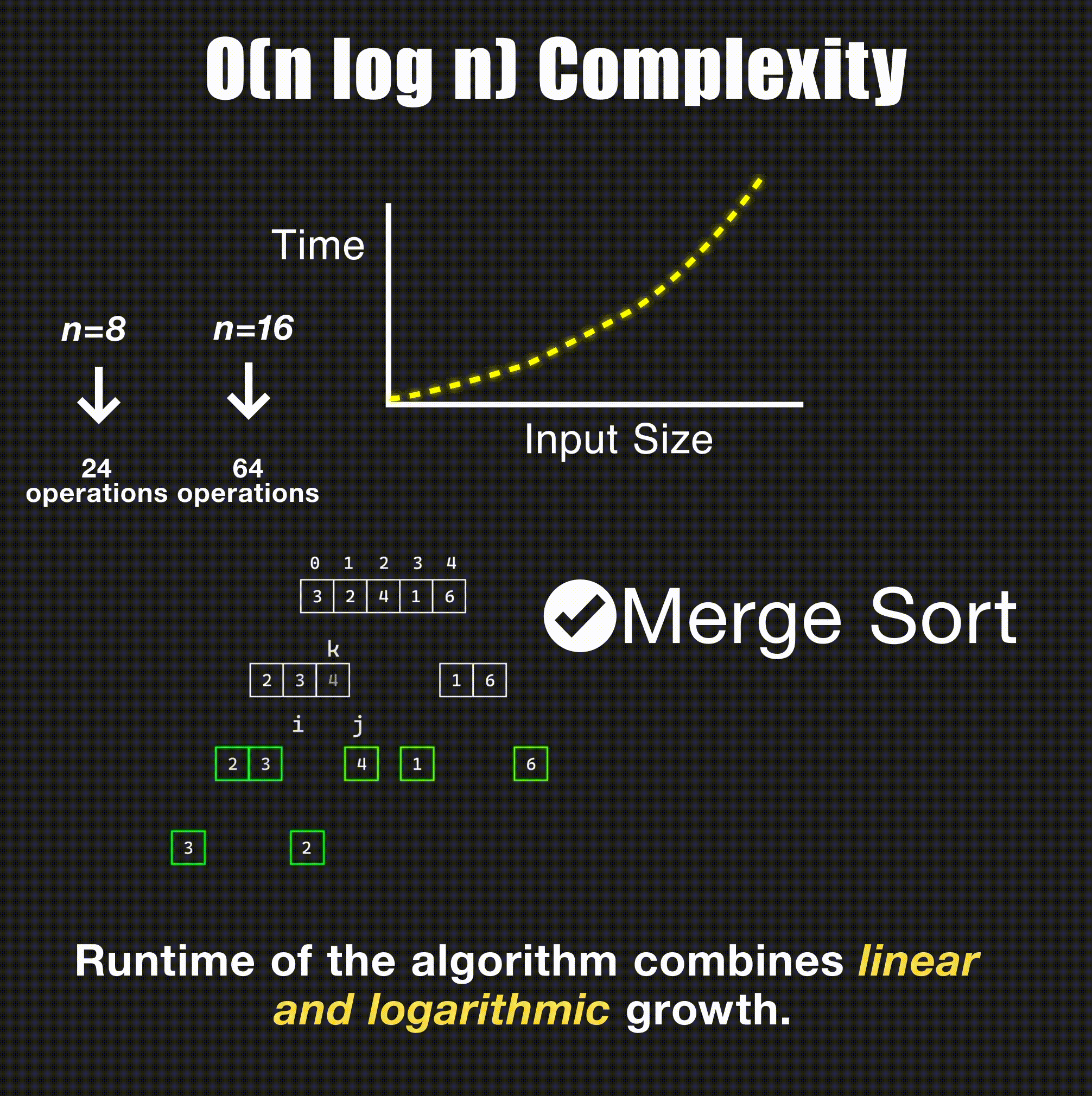
// Merge sort - O(n log n)
void mergeSort(int arr[], int left, int right) {
    if (left < right) {
        int mid = left + (right - left) / 2;
        mergeSort(arr, left, mid);
        mergeSort(arr, mid + 1, right);
        merge(arr, left, mid, right);
    }
}

// Merge sort - O(n log n)
public void mergeSort(int[] arr, int left, int right) {
    if (left < right) {
        int mid = left + (right - left) / 2;
        mergeSort(arr, left, mid);
        mergeSort(arr, mid + 1, right);
        merge(arr, left, mid, right);
    }
}

# Merge sort - O(n log n)
def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])
    return merge(left, right)

O(n²) - Quadratic Time

Nested loops - comparing each element with every other element

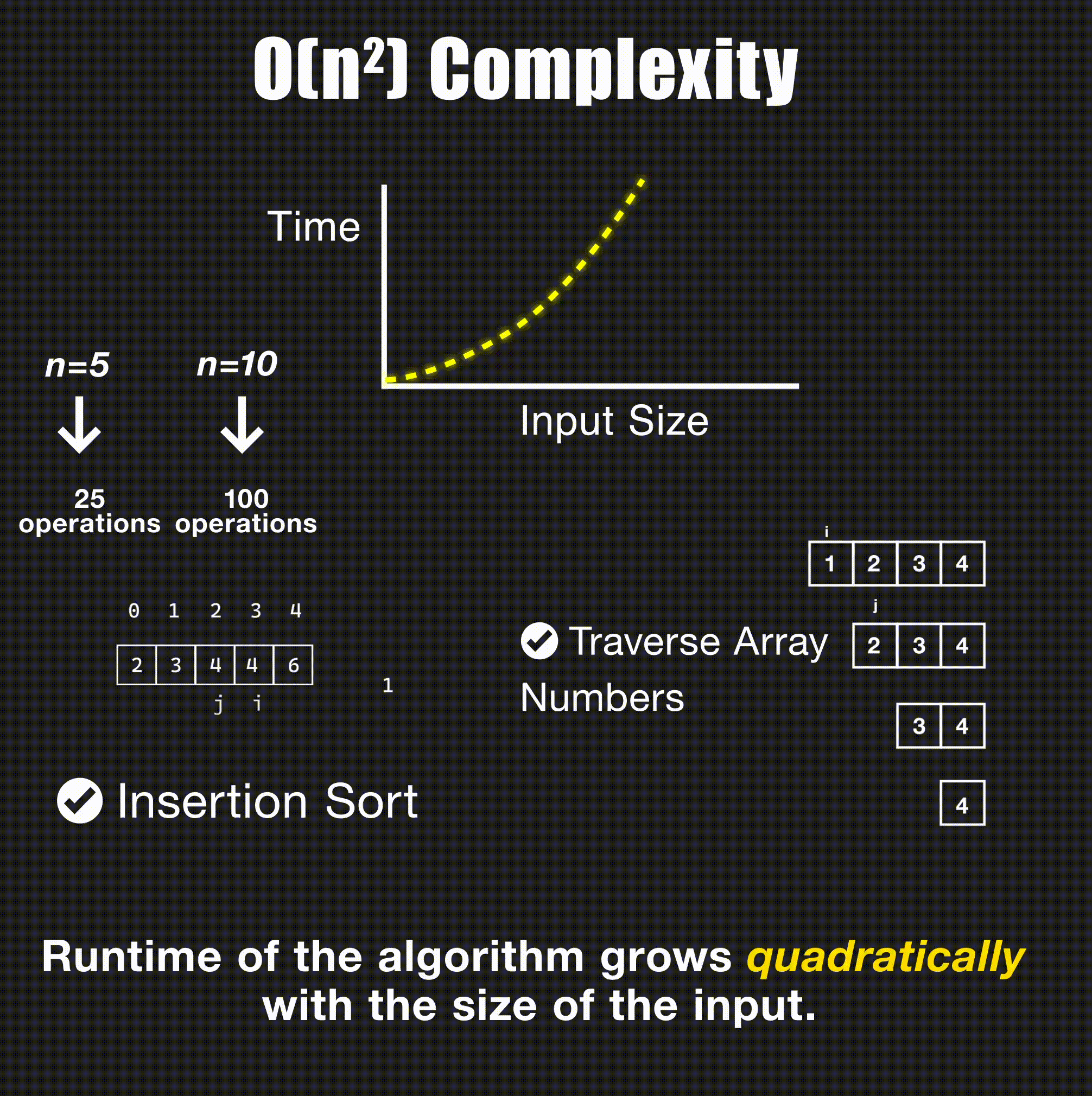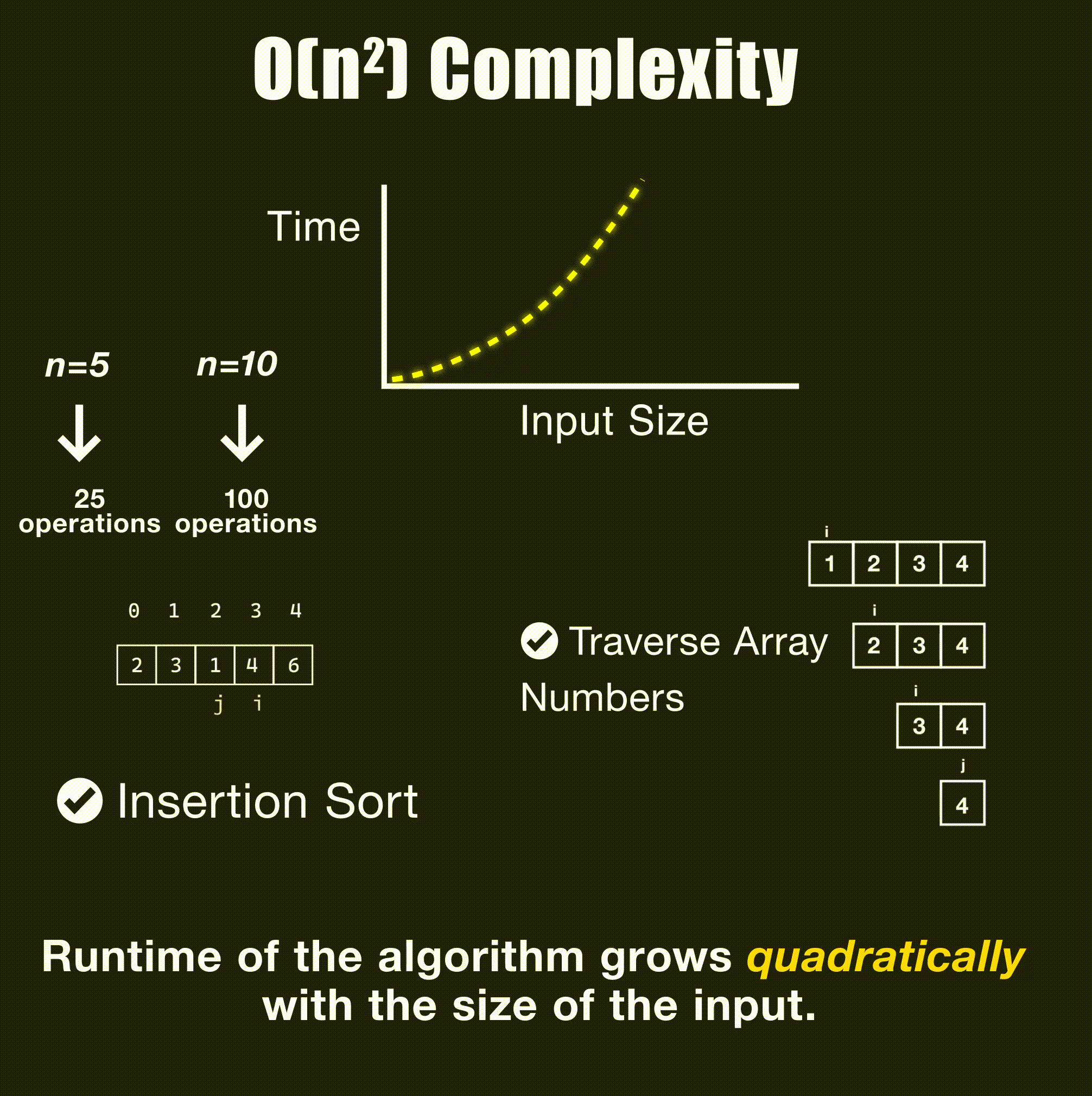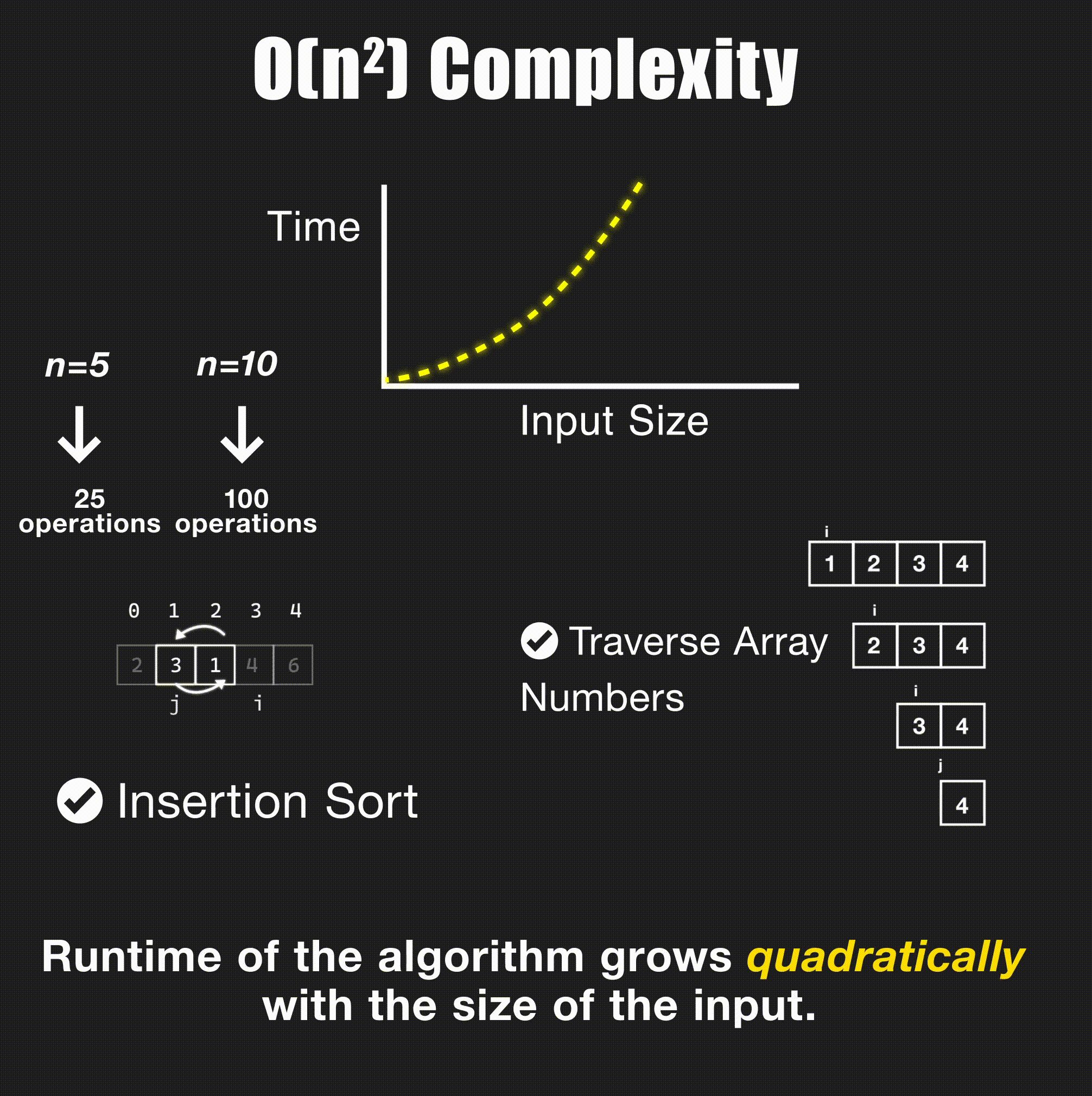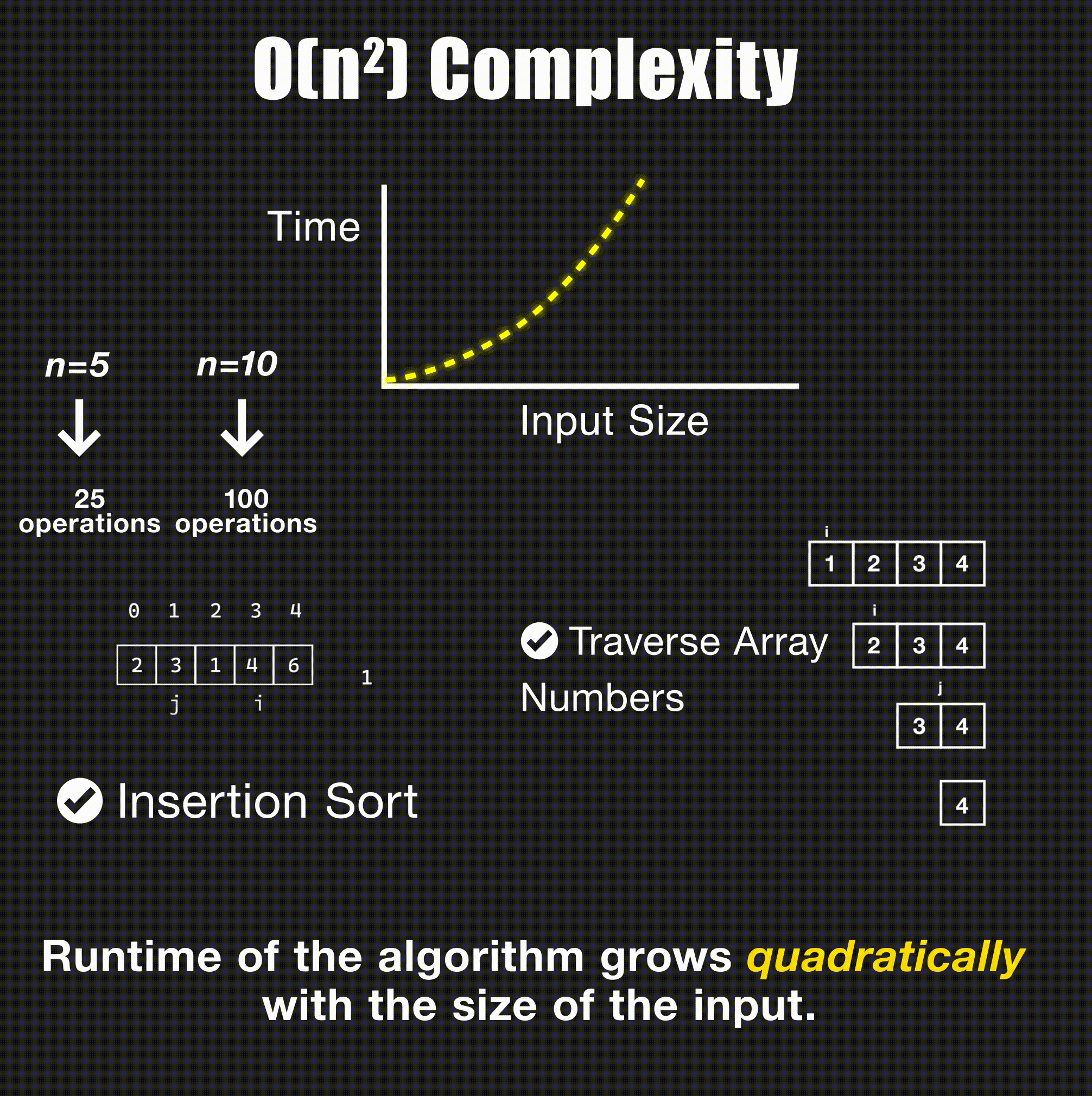
// Bubble sort - O(n²)
void bubbleSort(int arr[], int n) {
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                // Swap elements
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

// Bubble sort - O(n²)
public void bubbleSort(int[] arr) {
    int n = arr.length;
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                // Swap elements
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

# Bubble sort - O(n²)
def bubble_sort(arr):
    n = len(arr)
    for i in range(n - 1):
        for j in range(n - i - 1):
            if arr[j] > arr[j + 1]:
                # Swap elements
                arr[j], arr[j + 1] = arr[j + 1], arr[j]

O(N*M) - Linear with Two Variables

Processing a 2D matrix - time depends on both dimensions

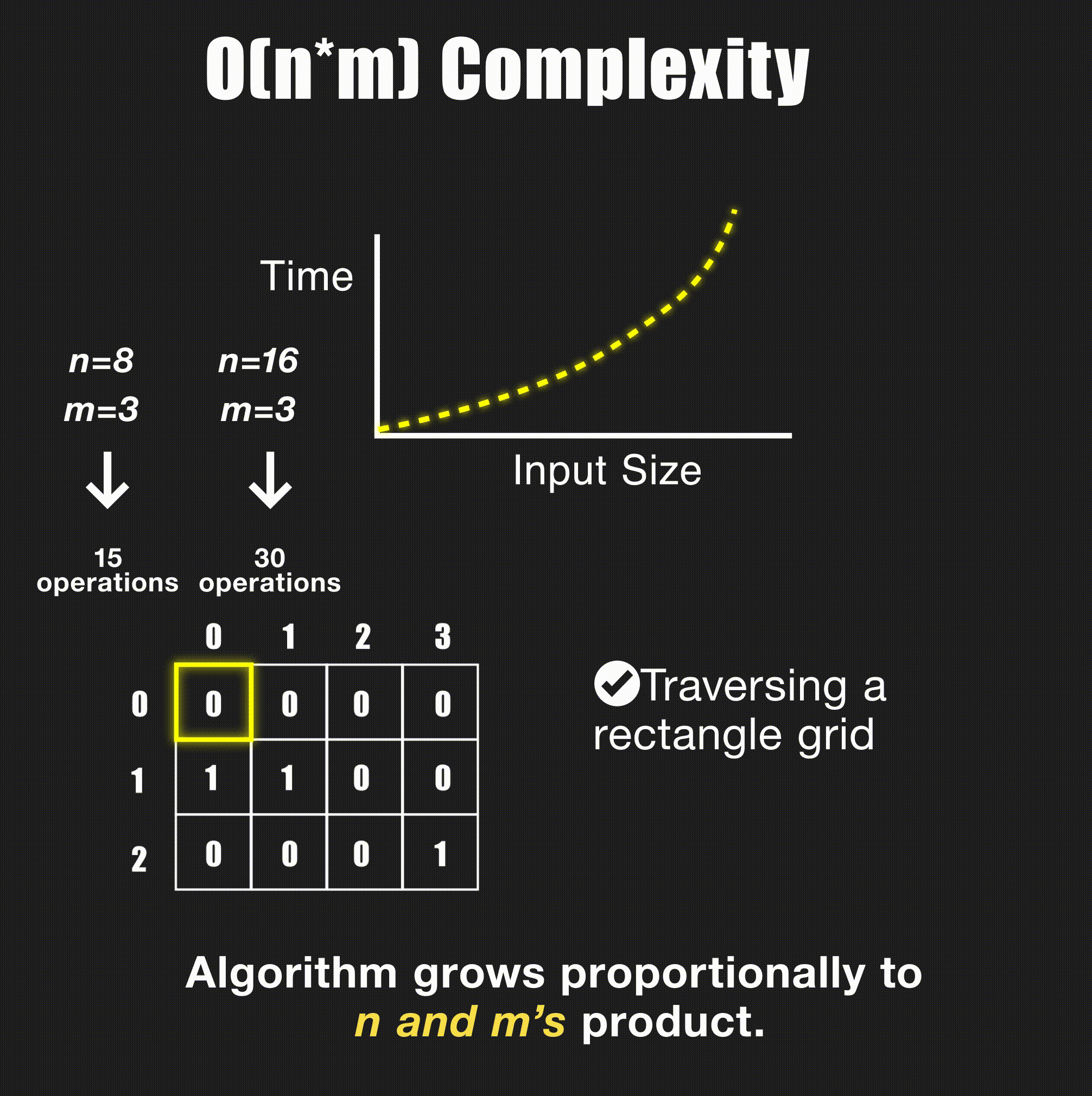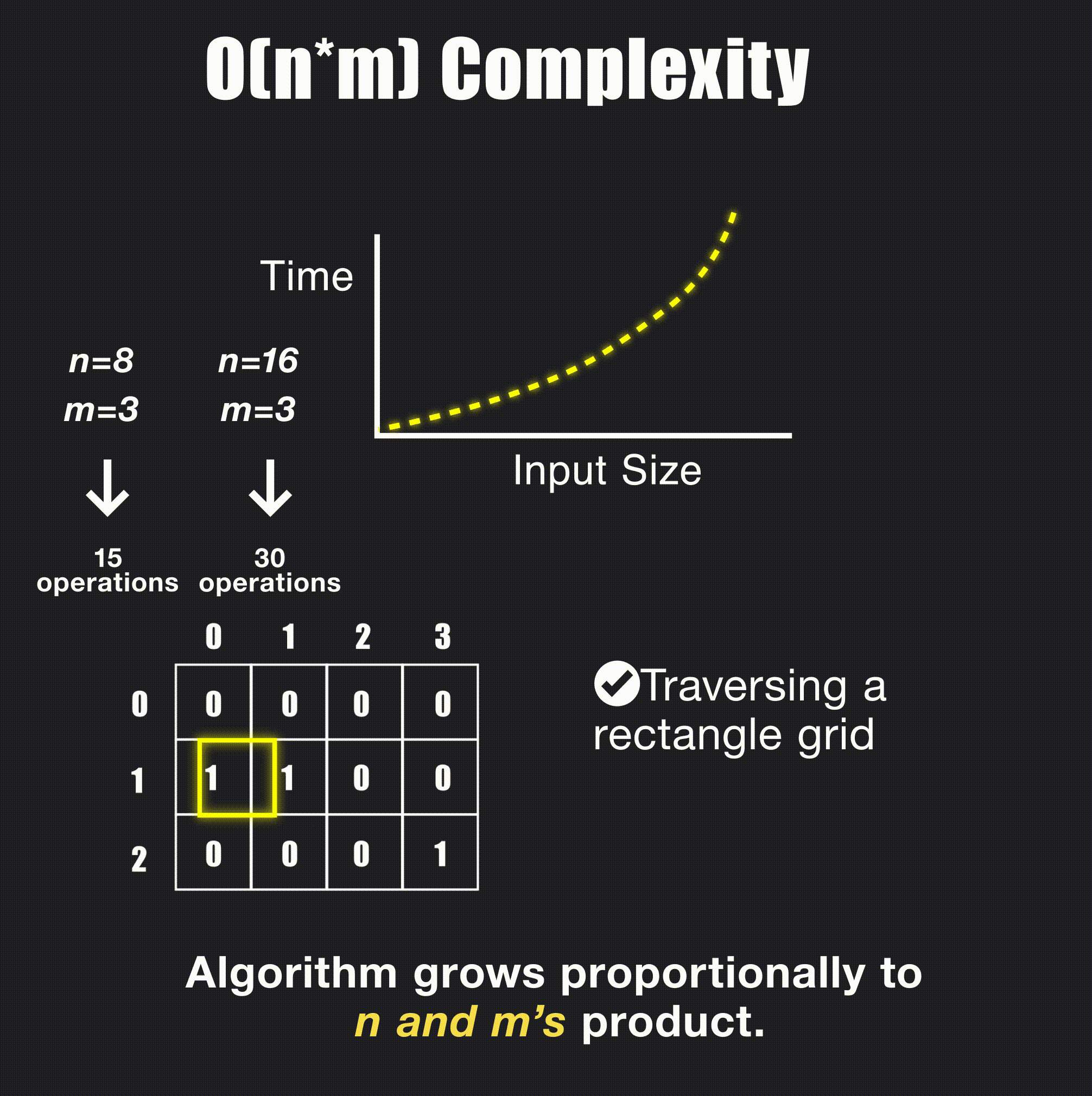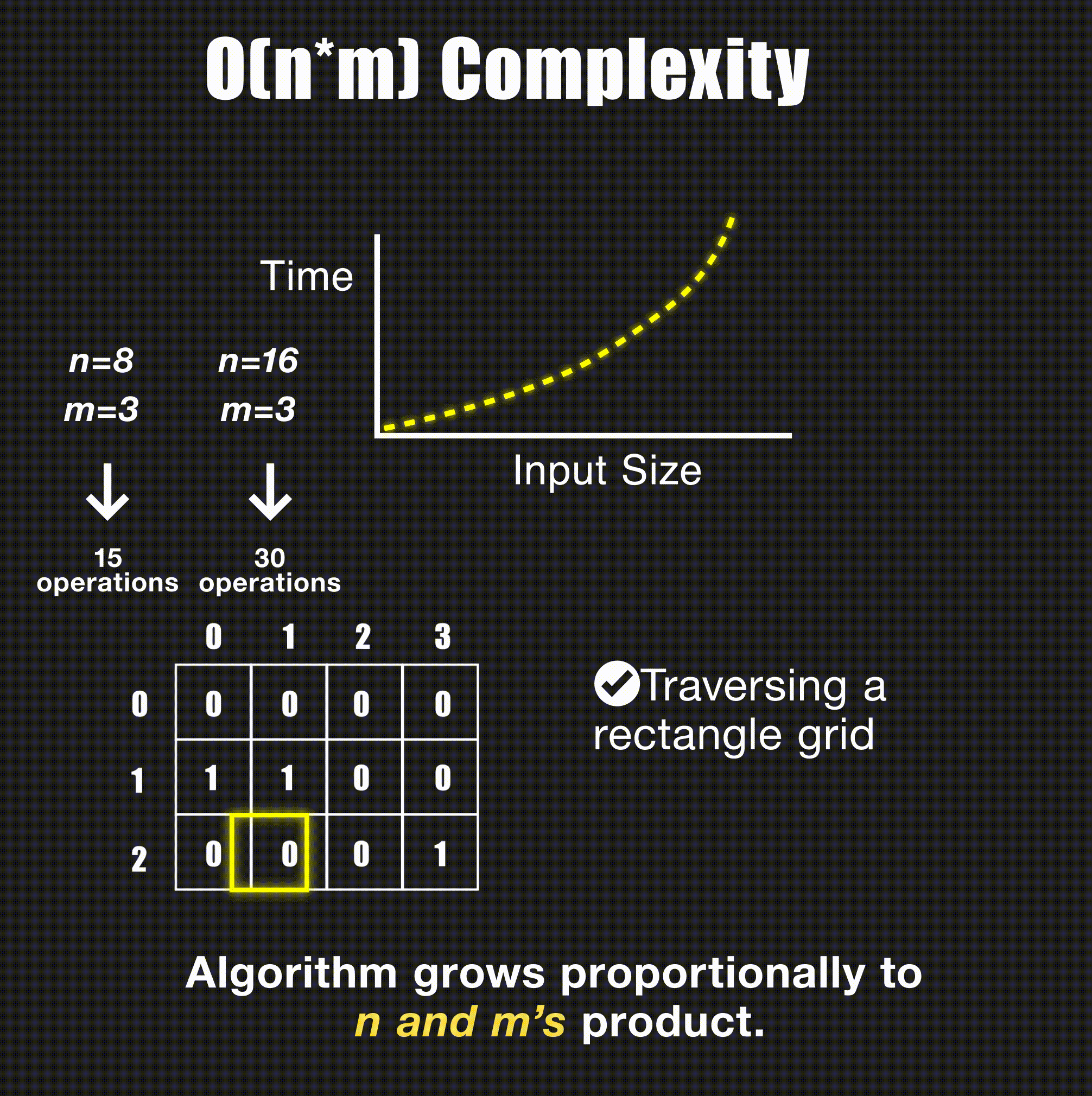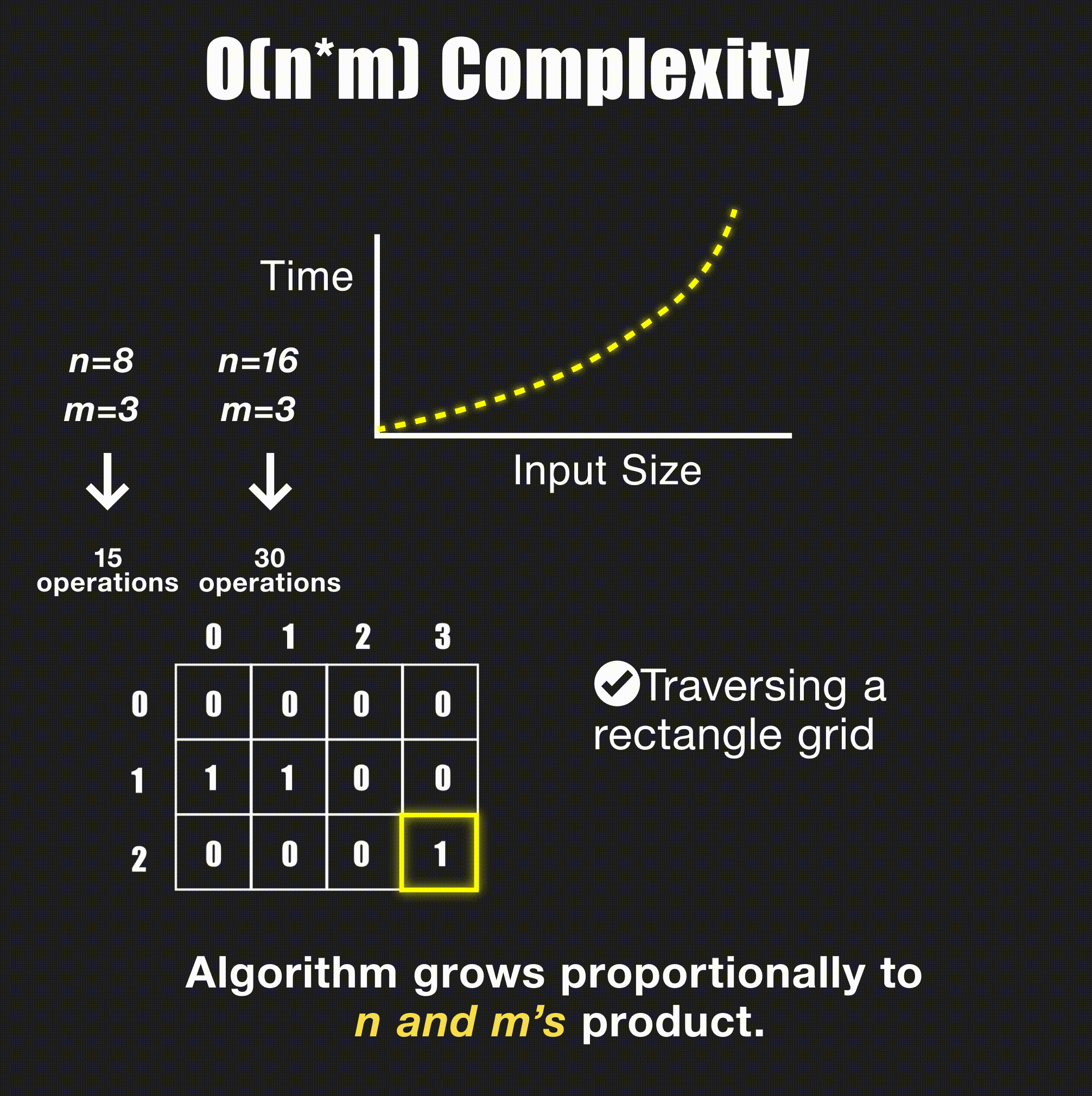
// Process 2D matrix - O(N*M)
void processMatrix(int matrix[][], int rows, int cols) {
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            // Process each element
            printf("%d ", matrix[i][j]);
        }
    }
}

// Process 2D matrix - O(N*M)
public void processMatrix(int[][] matrix) {
    int rows = matrix.length;
    int cols = matrix[0].length;
    
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            // Process each element
            System.out.print(matrix[i][j] + " ");
        }
    }
}

# Process 2D matrix - O(N*M)
def process_matrix(matrix):
    rows = len(matrix)
    cols = len(matrix[0]) if rows > 0 else 0
    
    for i in range(rows):
        for j in range(cols):
            # Process each element
            print(matrix[i][j], end=" ")

O(2ⁿ) - Exponential Time

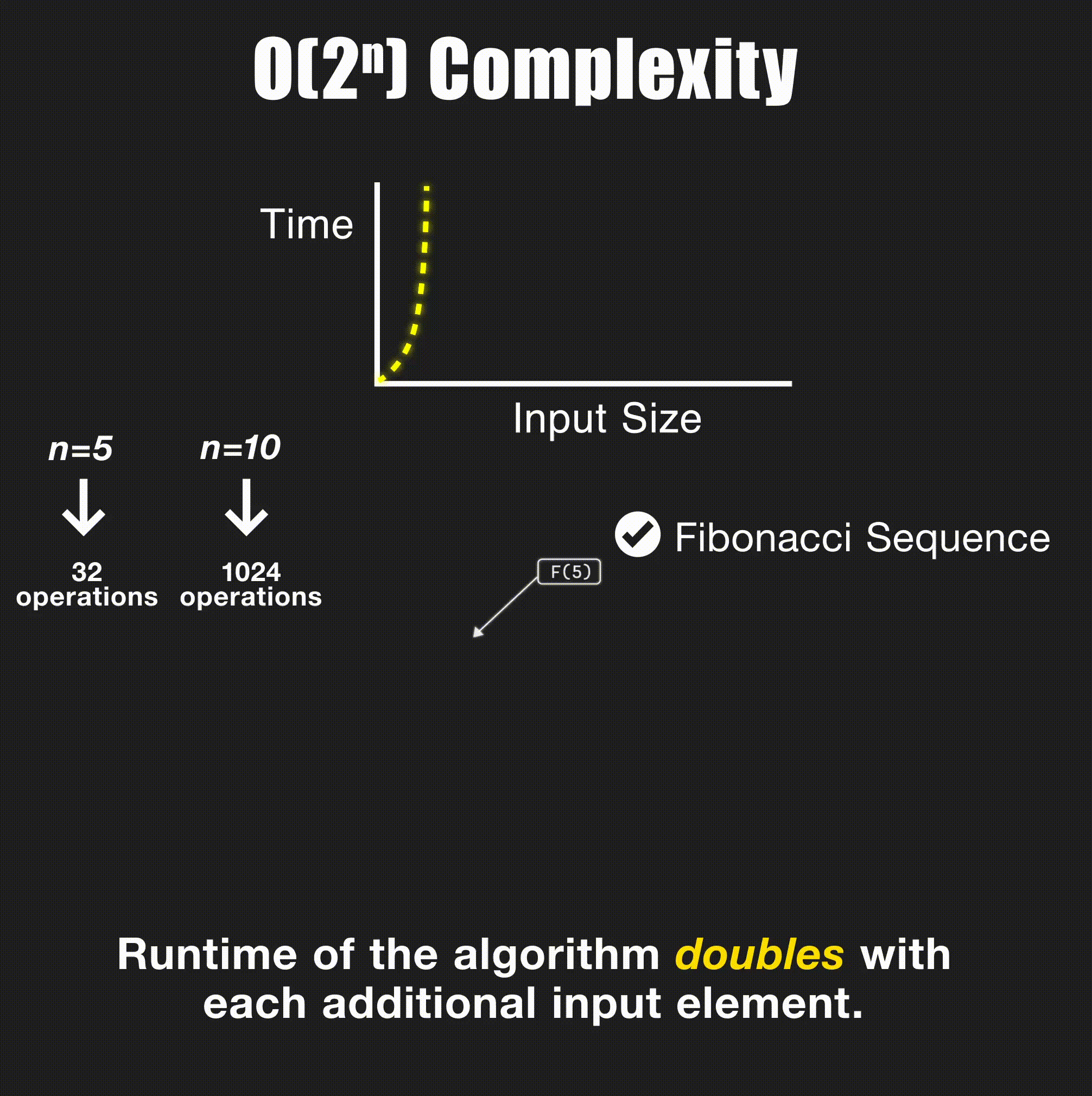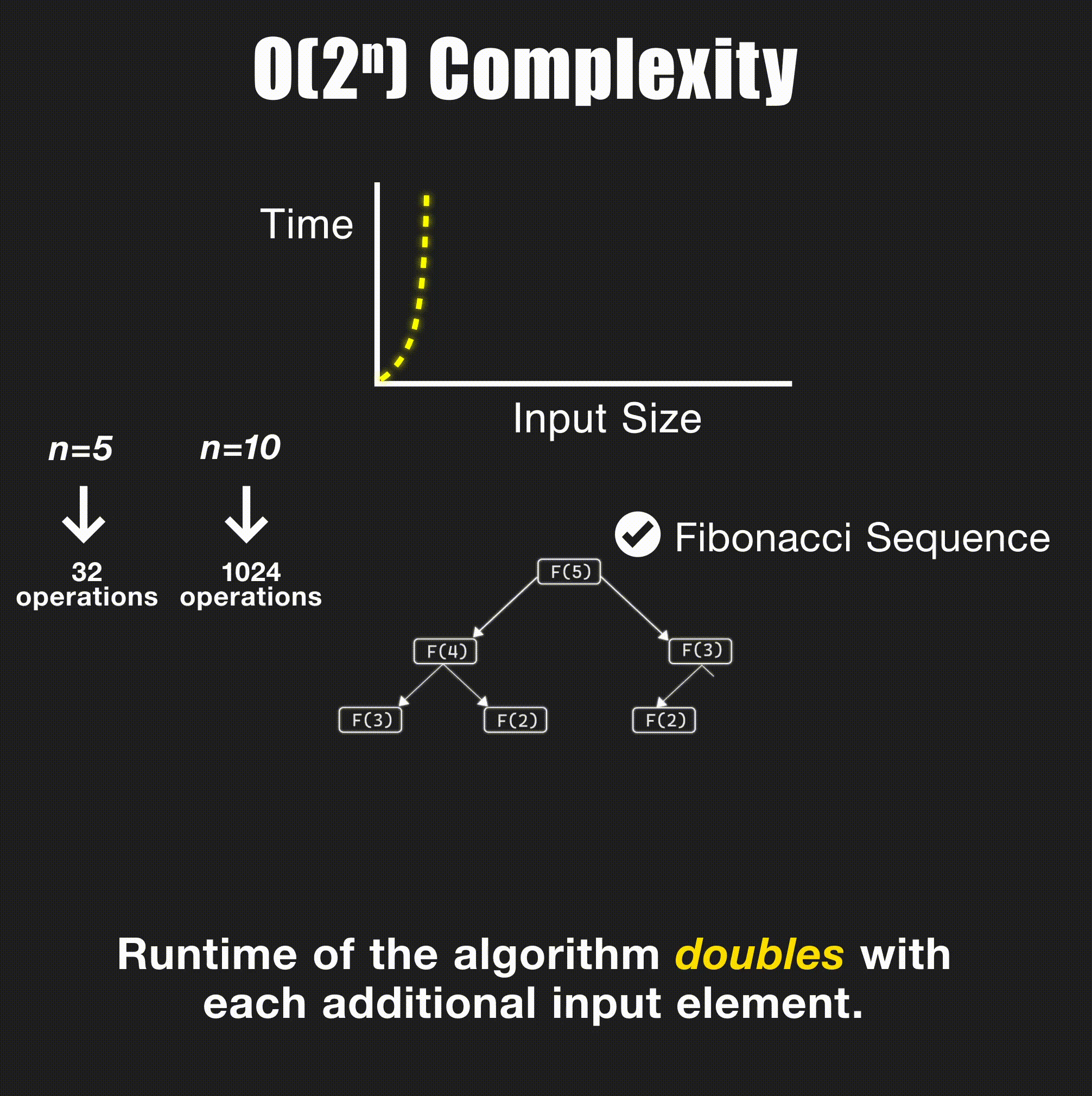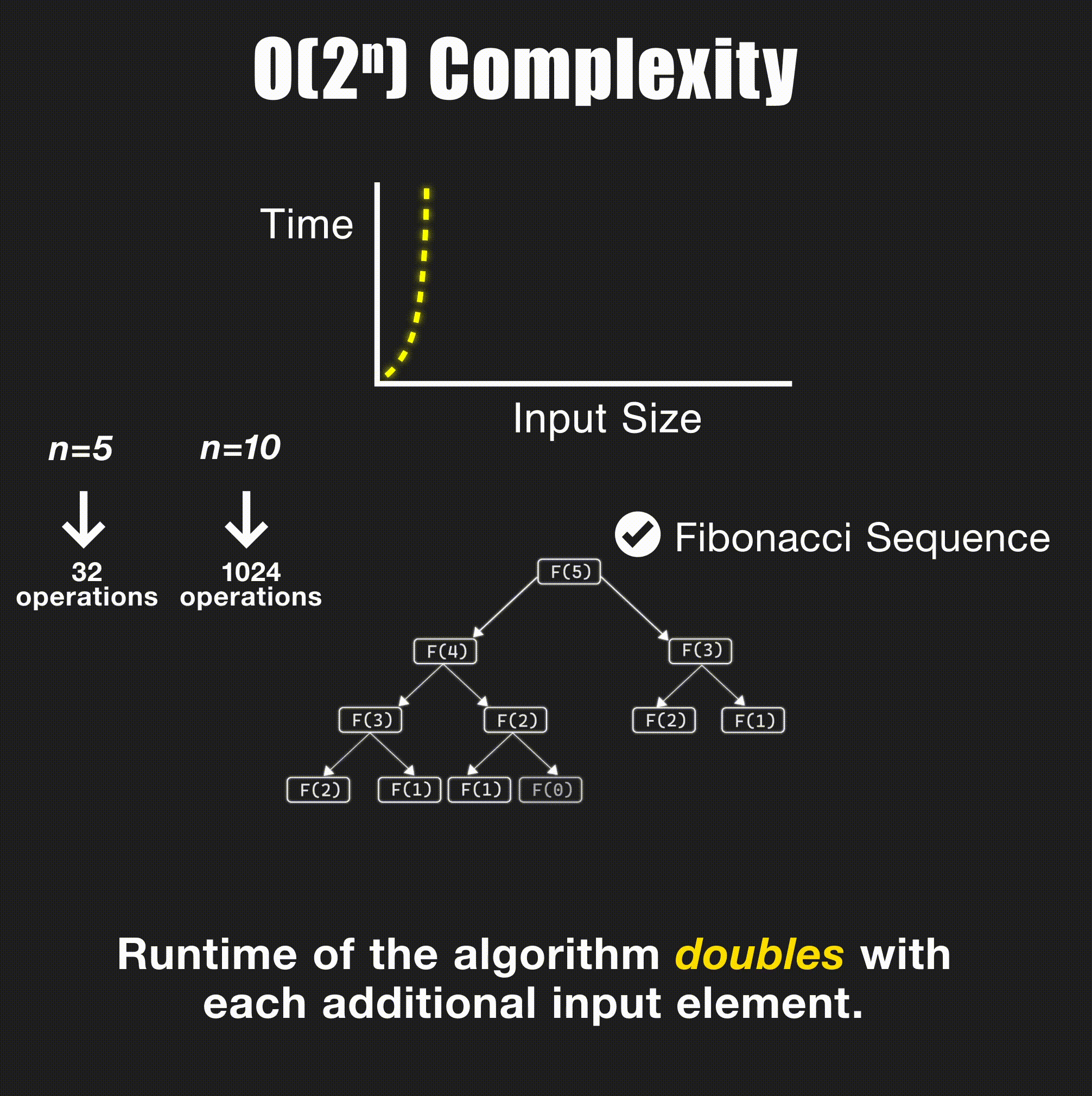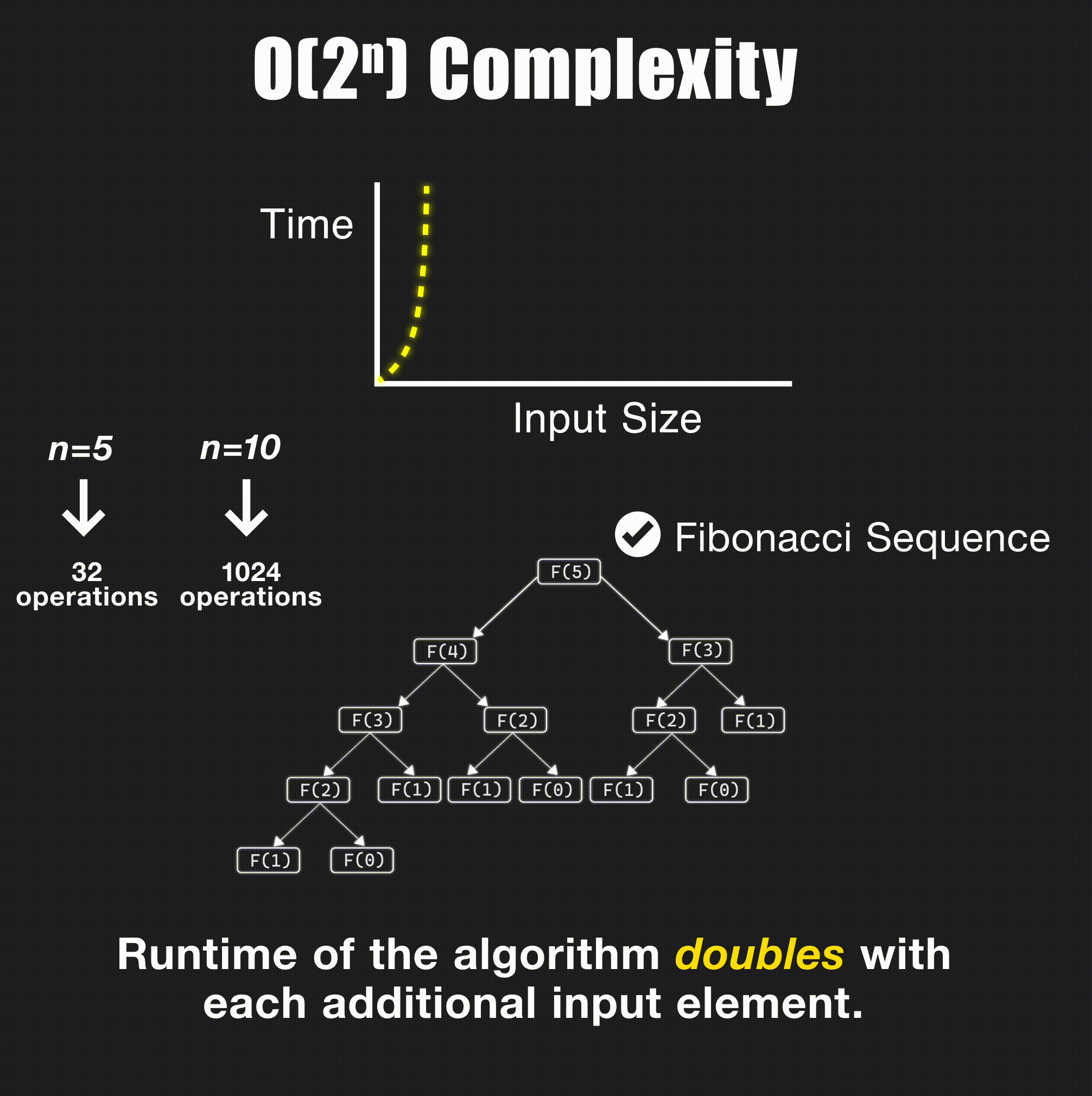
O(2^n) Exponential time complexity visualization

Generating all subsets - runtime doubles with each additional element

// Fibonacci (naive approach) - O(2^n)
int fibonacci(int n) {
    if (n <= 1) {
        return n;
    }
    return fibonacci(n - 1) + fibonacci(n - 2);
}

// Fibonacci (naive approach) - O(2^n)
public int fibonacci(int n) {
    if (n <= 1) {
        return n;
    }
    return fibonacci(n - 1) + fibonacci(n - 2);
}

# Fibonacci (naive approach) - O(2^n)
def fibonacci(n):
    if n <= 1:
        return n
    return fibonacci(n - 1) + fibonacci(n - 2)

Space complexity

Space complexity measures additional memory an algorithm uses relative to input size. For example, in-place operations often use O(1) extra space, while algorithms that build auxiliary structures may use O(n) space.

Cheat sheet

Operation	Time	Notes
Array index access	O(1)	Direct addressing
Array traversal	O(n)	Visit each element once
Binary search (sorted)	O(log n)	Halves search space
Efficient sorts	O(n log n)	Merge sort, quicksort (avg)
Naive double loop	O(n²)	All pairs comparisons

Takeaways

Think in growth rates, not exact times
Prefer lower-order complexities for scalability
Consider both time and space; constraints matter

Big O Notation (Time Complexity)

Why it matters

How to read Big O

Common growth rates

Quick examples

Visual examples

O(1) - Constant Time

O(log n) - Logarithmic Time

O(n) - Linear Time

O(n log n) - Linearithmic Time

O(n²) - Quadratic Time

O(N*M) - Linear with Two Variables

O(2ⁿ) - Exponential Time

Space complexity

Cheat sheet

Takeaways